Liberté et acquisition de concepts mathématiques, une incompatibilité originelle ?
Aucune approche exploratrice et ouverte ne serait possible pour une appropriation de concepts dans ce domaine réputé complexe, rigoureux et d’accès difficile ?
Notre longue expérience montre qu’il n’en est rien : la technique de la recherche libre s’applique également dans le domaine mathématique.

abstraction

  L’abstraction apparaît comme un processus cognitif élémentaire de traitement d’informations, de situations, qui opère dans  la constante et impérieuse nécessité pour chaque individu d’explorer son environnement et de s’y adapter.
Elle simplifie la réalité complexe en distinguant une ou plusieurs caractéristiques particulières d’un objet tout en délaissant les autres. Elle est à la base de la formation des concepts.
Elle permet également par la généralisation à classer des objets suivant ce qui leur est commun et à créer et identifier des catégories, des modèles, des structures.
Elle participe à la perception du monde, à sa découverte, sa représentation, sa compréhension, par le développement de la pensée, du langage, l’acquisition de connaissances, de savoirs…*
Mais pourquoi l’abstraction pose-t-elle tant de problèmes  à l’école dans le domaine des mathématiques ?

* voir partie 1, chapitre 4 « apprendre »

abstraction et concepts mathématiques

Les mathématiques apparaissent, pour le sens commun, comme le lieu ultime de l’abstraction.
Elles ne seraient qu’un jeu mystérieux avec des symboles, des relations, un langage, totalement étranger au monde sensible, ne laissant aucune place à l’affectif.
La personne et son statut de sujet, les autres, tout y semble exclu et les objets dépossédés de tout caractère propre.

abstraire, une définition

L’individu, par cette opération de l’esprit, réduit la complexité de la réalité (et ce, pour la perception, dès l’origine de son processus), la « simplifie » afin de mieux pouvoir l’appréhender, se la représenter et la communiquer aux autres.

Ainsi, dans la recherche « le bateau »*, les éléments principaux de l’événement sont cités lors de sa présentation devant la classe : la sortie en famille, le lac, le bateau, le temps qu’il a fait, mais tout n’est pas raconté. Certains éléments (la forme du bateau, , la couleur de l’eau…, le monde qu’il y avait, la durée … sont omis ou peu à peu délaissés. Dans la multitude d’infos disponibles pour l’événement lui-même,  un choix a déjà été fait par l’enfant lors de sa re-présentation aux autres enfants de la classe.
Chacun d’entre-nous aurait bien voulu être là et faire la balade en bateau ensemble. La discussion a abouti à la question (problématique) suivante : « Est-ce qu’on aurait tous pu (les enfants du niveau CP, de toute la classe, mais aussi les grands de la maternelle avec qui on fait des présentations de textes communes) partir en même temps ? »

Au fur et à mesure de la réflexion, de nombreuses propriétés du bateau sont mises de côté (son apparence, son type de propulsion (voiles ou moteur), la forme de la coque, en bois ou en fer,…) au seul profit de ce qui va dans le sens du problème à résoudre : c’est un bateau à deux places.
Cette opération cognitive procède au choix des éléments pertinents par rapport au but poursuivi.

L’abstraction peut, dans d’autres situations**, opérer différemment : elle privilégie les propriétés générales d’un objet ou ensemble d’objets au détriment de ses propriétés spécifiques. Elle nous aide à classer des objets selon leurs caractéristiques communes et à créer des catégories.

*voir la partie 2 des recherches/ le bateau »

**voir la partie 4 domaines math , « maths non numériques/relations »

Parmi tous les aliments, je suis capable de distinguer les fruits des autres denrées, les pommes des autres fruits, les Golden des autres pommes, etc.

  C’est la technique de la recherche libre mathématique* à partir d’événements tirés de la vie courante, de la classe, de créations ou de situations abstraites qui est choisie pour permettre la construction des savoirs. Elle est issue de la pédagogie Freinet et corroborée depuis par les apports du (socio)constructivisme** (Bruner, Vygotski) et de la théorie de l’autodétermination** (Deci & Ryan).
Elle place et accompagne  l’enfant dans des situations problématiques qui l’obligent à une réelle activité mathématique, activité qui va au-delà des simples constatations et découvertes de notions mathématiques. En effet, la seule fréquentation de situations recelant des notions maths ne suffit pas.
C’est lors du processus de résolution que des choix de stratégies sont faits, que la montée naturelle en abstraction et la symbolisation accompagnent la recherche des représentations appropriées, témoins de l’avancée, de l’état de la réflexion en cours et conformes au but poursuivi.
C’est dans cette montée en abstraction, impulsée et alimentée par une nécessité métacognitive d’analyse de ce qui se fait , que se construit la culture mathématique.
C’est la communication au groupe classe (présentation de la recherche) et les échanges à l’intérieur de celui-ci, qui favorisent la conceptualisation, la généralisation et la transférabilité des savoirs.
Là est la véritable activité mathématique, dans un processus de résolution qui aboutit à des savoirs intégrés (contenus et démarches) parce que construits et porteurs de sens.

*voir partie 1, chapitre 7 : la recherche libre mathématique

**voir partie 1, chapitre 3 : apprendre

l’objet mathématique, une pure construction de l’esprit

Les abstractions mathématiques se construisent sur une expérience sensorielle « concrète ». Mais les caractéristiques, les relations qui sont  retenues sont ensuite représentées par des symboles qui s’éloignent du réel perçu.

Les abstractions mathématiques ne concernent plus les objets eux-mêmes, mais les symboles qui les représentent.
Ces symboles, nouveaux objets d’étude, à leur tour vont s’articuler entre eux à la suite de nouvelles abstractions qui produiront de nouveaux symboles et ainsi de suite. Cette montée en abstraction s’éloigne de plus en plus du monde sensible pour peu à peu le potentialiser presque totalement.

Toujours dans la recherche « le bateau« , la mise à l’écart progressive de nombreuses caractéristiques de  l’événement amène à la conservation d’un seul attribut : c’est un bateau à deux places.
Cette opération cognitive procède au choix des éléments pertinents par rapport au but poursuivi. La « simplification » du réel adoptée aboutit à la découverte d’une solution experte spécifique à cette situation : s’il en reste 0 dans le groupement par deux, tout le monde peut partir en même temps.

Par la suite, d’autres situations de recherche (apparemment) différentes – se ranger par deux, danser par deux, le jeu du cheval, beaucoup d’activités en EPS (judo, raquettes, tennis de table,…) mais aussi le stylo à poussoir qui rentre et sort la pointe, l’interrupteur, le manteau retourné (à l’envers), les nombres pairs et impairs, et aussi les compositions de transformations géométriques (plusieurs symétries d’axes parallèles à la suite, rotations (½ tours successifs) – aboutissent à une conclusion identique : l’importance de la parité.
Une analyse de toutes ces situations conduit à la création d’une classe de situations équivalentes possédant la même technique de résolution et de décision : le rangement par deux et la prise en compte du reste. Ce concept mathématique porte un nom : c’est le modulo 2. Il a été  symbolisé dans la classe par :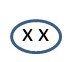         

Toutes les découvertes faites lors de la recherche le bateau s’appliquent à la résolution de toutes les situations problématiques de la même classe d’équivalence, qui relèvent donc du concept de modulo 2.
Cette généralisation apparaît comme le produit final cette recherche qui passe alors dans la mémoire à long terme de l’individu et du patrimoine collectif de la classe.
Mais la montée en abstraction peut se poursuivre : d’autres concepts – modulo 3, modulo 12, modulo n – sont construits  et généralisés sous le concept plus global de « modulo** », prêt à être mobilisé et utilisé dans d’autres contextes particuliers.

* voir  partie 2 : des recherches/ le bateau
** voir partie 3 : didactique/ abstraction et partie 4 : domaines math/fonctions numériques

une démarche d’apprentissage de l’abstraction : Britt-Mari Barth

Britt-Mari Barth*, professeure et chercheuse, a développé sa réflexion sur le processus enseigner-apprendre, sur le rôle de l’abstraction dans l’acquisition des connaissances. S’appuyant sur les travaux du chercheur américain Jérôme Bruner, elle propose une conception de l’apprentissage de l’abstraction basée sur la construction de concepts abstraits par l’apprenant**.(Ce résumé est extrêmement simplifié.)

Cet apprentissage se déroule en plusieurs étapes :
– la familiarisation avec les concepts : découvrir progressivement la structure d’un concept en cherchant des similarités entre situations, en les regroupant suivant des critères choisis subjectivement, puis en prenant conscience des caractéristiques d’un objet, d’une situation, en faisant  la distinction entre ses attributs essentiels et secondaires, en utilisant un symbole, un nom pour le représenter.
– l’acquisition de concepts :
rechercher, identifier les attributs principaux selon lesquels un concept est déjà défini, vérifier la règle de classification, puis savoir généraliser à partir d’un élément de la classe ;
– le transfert :
utiliser l’acquisition dans d’autres situations
–  la généralisation
L’apprentissage de l’abstraction passe par un entrainement systématique des élèves aux différentes phases de cette construction (entrainement à la perception, à la comparaison, à l’inférence et sa vérification, à la formation d’une hypothèse et sa vérification)

B-M Bart insiste sur le rôle essentiel de l’enseignant qui fournit un environnement stimulant et soutient activement le processus de construction du savoir de l’apprenant.

* « L’apprentissage de l’abstraction » Retz, 2001 (réédition)  « Le savoir en construction« , Retz, 1993
** voir la partie 1 la recherche ?, chapitre 3 apprendre/le socioconstructivisme

notre démarche

Nous partageons avec B-M Barth de nombreux aspects de sa réflexion à propos de l’abstraction.
Le choix de la construction des concepts par l’élève favorise sa plus grande implication.
Cependant, pourquoi se priver, en ne partant que de situations « scolaires »  choisies par l’enseignant et pas forcément motivantes pour tous, de l’énergie globale de l’individu, plus puissante, qui se manifeste lors du traitement de situations issues de la vie personnelle plus affectives, plus proches, de chacun ?
En effet, la dynamique qui aboutit à la manipulation de symboles, à la pure abstraction, s’appuie au départ sur l’expérience personnelle (la perception par les cinq sens, l’affectif, la culture première de chacun,…) totalement ancrée dans le monde environnant. Ce vécu peu à peu se potentialise* (n’est plus apparent mais toujours présent en arrière-plan et disponible) au fur et à mesure de la montée en abstraction, du tri, de l’abandon des éléments non pertinents par rapport à la cohérence et aux buts poursuivis.
 Aux représentations du monde perçu se substituent d’autres modèles, structures basés sur des invariances, des différences relevées et exprimées de manière symbolique et qui aboutissent à la construction d’un nouveau langage, le langage mathématique.

  Et pour que ces constructions puissent se faire,  pourquoi ne pas permettre à chaque apprenant de suivre son propre cheminement dans un processus de recherche  dont il se sent être à l’origine, qui n’est pas au-delà de ses capacités, qui lui donne le sentiment d’efficacité et la possibilité d’être valorisé par d’autres éléments du groupe classe.

   C’est pendant ce processus de résolution que les représentations à adopter, les orientations à suivre, les essais à tenter contraignent le chercheur à un regard métacognitif sur son activité : quels sont les chemins qui mènent aux réponses recherchées ? Quelles sont les solutions échafaudées les plus efficaces, les plus économiques, les plus élégantes ? Les réussites avérées, petites ou grandes, nourrissent les  patrimoines de la classe. Elles peuvent devenir des références pour d’autres recherches. Il faut apprendre à apprendre.

Des moments collectifs menés par l’enseignant ont pour objet de synthétiser les découvertes, les classifications et unifications de situations, de procédés de résolution et ainsi accéder à la formalisation de concepts mathématiques et à leur généralisation.

C’est l’ambition de la technique de la recherche libre mathématique que de susciter la motivation autodéterminée de chaque jeune chercheur dans la construction et la mobilisation des concepts mathématiques.