Le drôle de papa
école : classe unique (section enfantine, cycle 2 et 3 : enfants de 5 à 11 ans
niveau concerné : cycle 2
recherche individuelle : Mickaël, entre 5 ans 1/2 et 8 ans.
domaines : géométrie de transformation, symétrie axiale
connexions : axe, symétrique, machine, distance,

Bertrand, 5 1/2 ans, présente dans son texte « un drôle de papa » qui a une oreille ronde et une autre carrée, un petit bras et un long bras, un bras bleu et l’autre rose, six jambes. (trois et trois).
Il propose d’autres productions sur le même thème.
Il poursuit l’idée de son texte en inventant d’autres exemples : des papas, un papa sans tête, des papillons, oiseaux…
Puis il revient à des êtres « qui ne sont pas drôles ». On les appelle papa symétrique, papillon symétrique,…

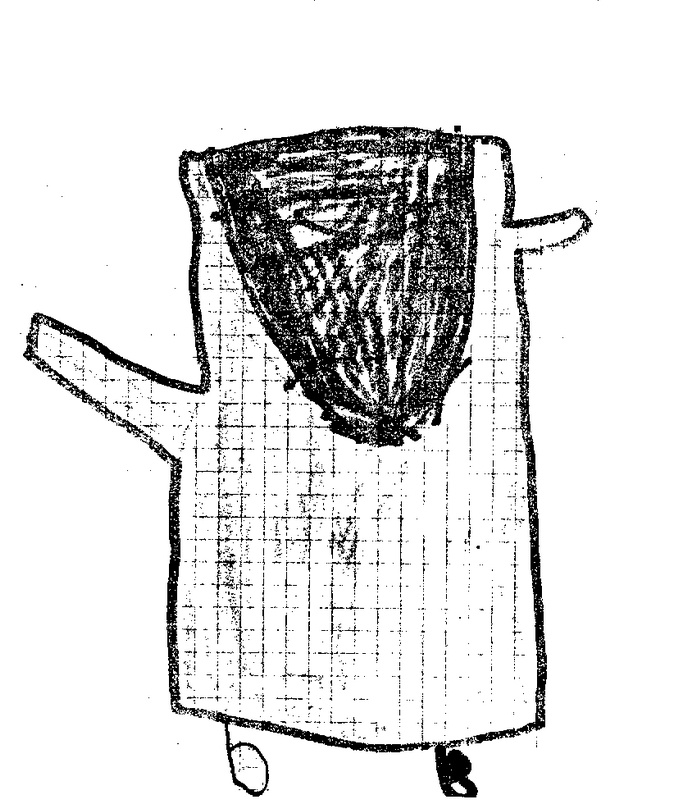





Lors de la présentation de ce début de recherche, il s’est avéré qu’un enfant de cinq ans n’a pas eu de problème pour compléter une bête symétrique ou un soleil symétrique :

Sa production, bien que maladroite, convient parfaitement aux plus jeunes. Il semble donc que certains enfants, à cet âge, ont déjà potentialisé quelques invariants de la symétrie comme la conservation de la forme, de la taille et de certaines directions.
La symétrie s’actualise dans la conscience de l’observateur quand elle est prise en défaut : on remarque plus facilement un manchot qu’un individu constitué « normalement ».
L’idée de Bertrand suscite l’intérêt des enfants les plus jeunes : on veut inventer d’autres « drôles de papas ». Mickaël propose un drôle de papa : « Il a une chaussure plus grande que l’autre. » D’autres idées de drôles de papas sont avancées, et d’autres « drôles de … » sont suggérés.
C’est donc Mickaël qui reprend, à la suite de la présentation de Bertrand, l’idée que celui-ci laisse de côté momentanément pour une autre recherche. Il peut démarrer son travail individuellement avec son drôle de papa et quelques autres idées de la classe qu’il a retenues.
Mickaël travaille sur des feuilles A4 qui seront scotchées les unes aux autres en accordéon. Il connaît cette technique du dépliant, et avec ses idées et celles du groupe, il est autonome et peut commencer.
Pour l’instant, on ne parle pas de recherche : il doit juste représenter les diverses propositions formulées et si possible, en inventer d’autres.


Voici le drôle de papa de Michaël : il a une chaussure plus grande que l’autre. Puis le papa normal, baptisé papa symétrique (sur ma proposition)
La symétrie du corps semble bien intégrée puisque le jeu des drôles de papas consiste justement à la déjouer.
Ont suivi les drôles de fleurs, de papillons, de soleils … et leurs homologues symétriques.
Ces réussites se construisent sur une connaissance «intuitive», plus ou moins consciente de la symétrie du corps.
Mathieu, après quelques mois d’existence, sait présenter un bras, puis l’autre, pour l’habillage et le déshabillage. Il sait qu’on met deux chaussures. Quand il découvre ses oreilles, il touche l’une puis l’autre et vient vérifier si j’ai bien une oreille d’un côté, puis une oreille de l’autre. Même chose pour les yeux…
Jusqu’à présent, l’objet de la recherche n’est pas encore déterminé avec précision.
Premiers tâtonnements
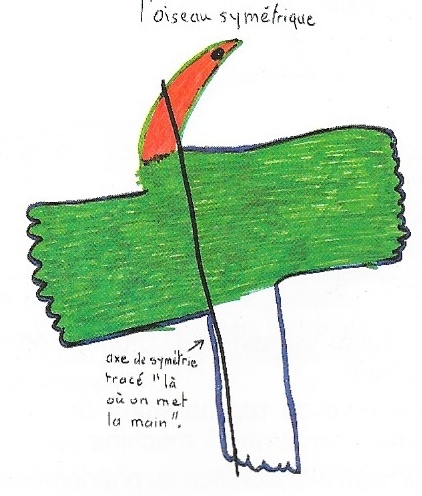
Michaël peut donc, en se référant à cette connaissance de la symétrie du corps qu’il a dû se construire alors qu’il était bébé et qui s’est renforcée lors de l’apprentissage de la marche, dessiner un drôle d’oiseau (une aile plus grande que l’autre) ou un oiseau symétrique.
Après observation plus précise, force est de constater que ce n’est pas « pareil » de chaque côté, le « pareil » restant pour l’instant une expression floue. Bien sûr, l’exploration de la signification de ce pareil amènera à la découverte des invariants de la transformation.
On dit « pareil de chaque côté », mais où sont les deux côtés ? Où est la limite ? Michaël place sa main pour me montrer. Mais dès que la main est retirée, il n’y a plus de trace… Il dessine donc une ligne qui sera immédiatement appelée axe de symétrie.
Nouvel essai :
Après examen du résultat, des imperfections subsistent encore : le bec de la moitié « objet » (droite) est plus haut que celui de la partie « image » (gauche). L’aile est trop petite, la queue, ça ne va pas. La « machine » dessin à main levée montre ici ses limites. Il faut en trouver une autre, plus performante.
L’objet de la recherche se précise : il faut être capable de produire un objet symétrique le plus fidèlement possible.
Début de recherche
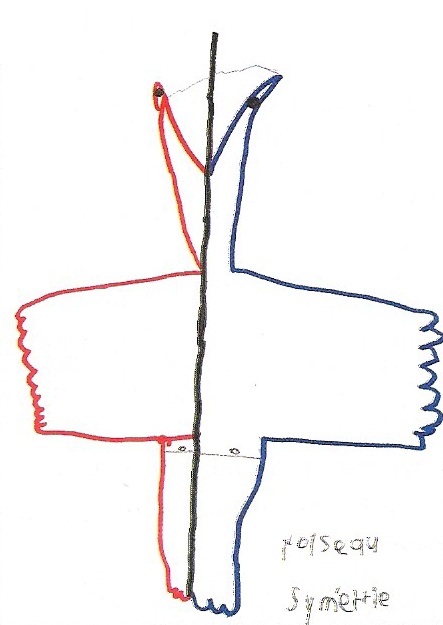
Nouveaux essais, puis je lui propose de ne dessiner que la moitié de l’oiseau et de compléter ensuite la partie symétrique.
Pour se souvenir de la moitié « départ », on décide d’utiliser le bleu et le rouge pour la deuxième partie (patrimoine mathématique de la classe). Par la suite, on les a respectivement nommées « objet » et « image ».
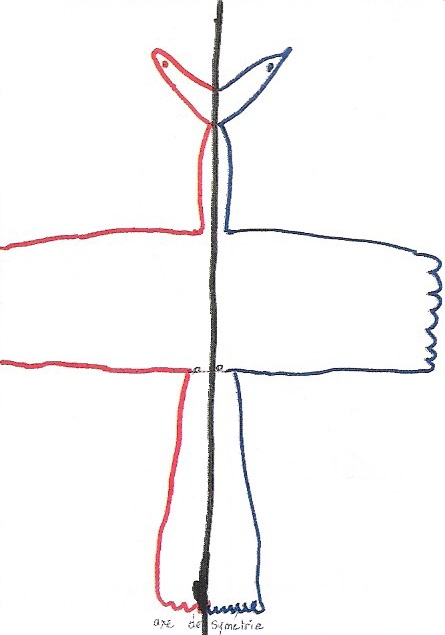
Une stratégie se dessine : pour que les deux côtés soient « pareils », il faudrait amener la partie bleue de l’autre côté. 0n fait donc un pli le long de l’axe de symétrie et on admet que pendant l’opération de rabattage de la demi-feuille, la partie bleue ne subit aucune transformation de type agrandissement ou diminution. Pour reporter le contour bleu, on utilise une pointe de compas et on « décalque » en perçant des trous. Il n’y a plus qu’à repasser en suivant les petites perforations.
Michaël s’entraîne à cette technique nouvelle. Je lui propose deux dessins à compléter (papillon, oiseau).
Puis il continue tout seul. Il fait beaucoup d’autres exemples.
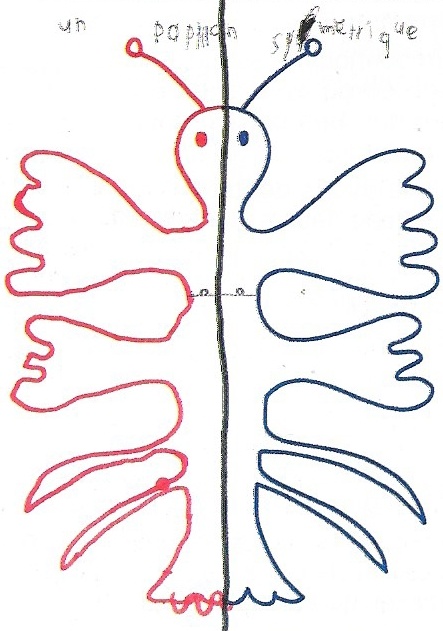
Découverte d’une « machine* »
La « machine » peut être apportée par l’enseignant.
Exemples : une machine traçante comme le pantographe pour les homothéties, une calculette pour les fonctions numériques, un disque en carton (style disque de stationnement) pour les fonctions périodiques.
* machine : technique opératoire matérielle
Première présentation
Michaël présente et explique sa recherche. (A ce moment-là, les axes de symétrie ne sont pas encore tracés.)
Pour les premiers dessins, Michaël parle de « pareil des deux côtés » et de « pas pareil des deux côtés ». Légère hésitation d’Amandine qui pose la question : « Mais où sont les deux côtés ? »
Apparaît alors la nécessité de montrer où on place la main à chaque fois, ou mieux, de tracer l’axe de symétrie. C’est ce que Michaël va faire par la suite, sur les premiers dessins (ligne noire).
Puis Michaël explique la technique utilisée pour obtenir des dessins bien symétriques. Chacun veut essayer.
De nombreux objets symétriques sont produits soit à partir d’un demi-dessin à compléter, soit librement. Produire soi-même la première moitié du dessin est une activité qui réserve de nombreuses surprises et amène de nouveaux éclairages sur le phénomène.
Le symbole ![]() a été placé sur ces dessins ultérieurement.
a été placé sur ces dessins ultérieurement.
Après des essais plus ou moins satisfaisants « à la main », Mickaël a réussi à reproduire le phénomène à l’aide de la « machine » pliage-pointe.
Une autre machine sera découverte par la suite, un peu plus rapide : on obtient l’image, après pliage de la feuille, non plus avec les points percés mais par transparence en posant celle-ci sur une vitre.
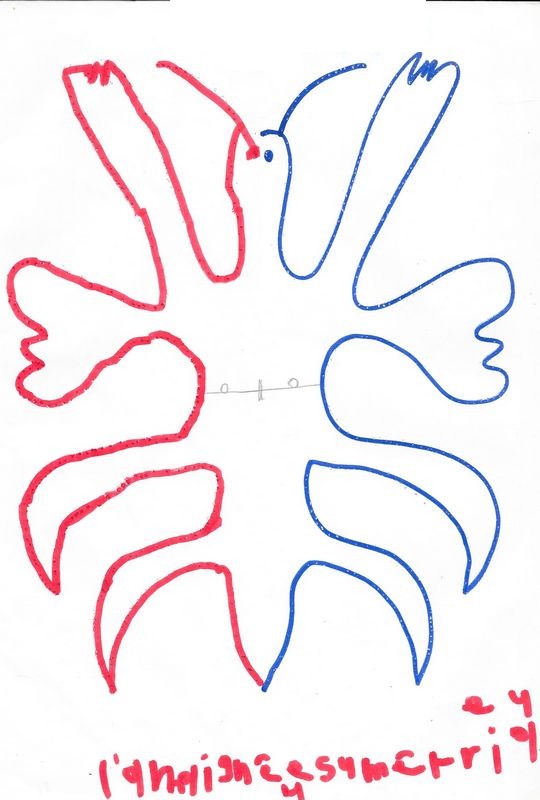
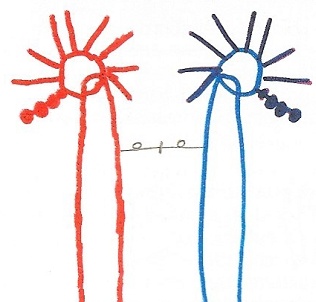
Des monstres naissent.
Quelquefois des silhouettes plus familières apparaissent : araignées, aigle ou… fantôme.
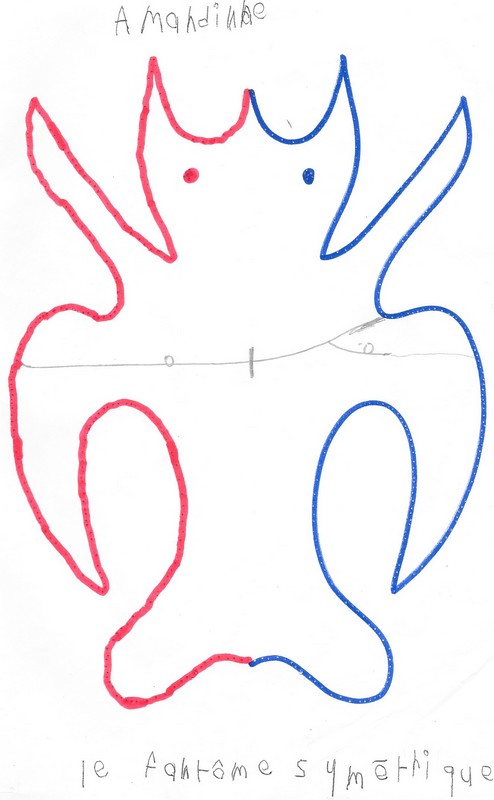
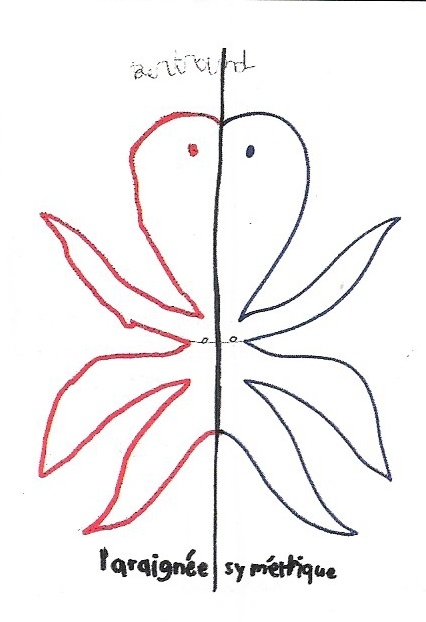
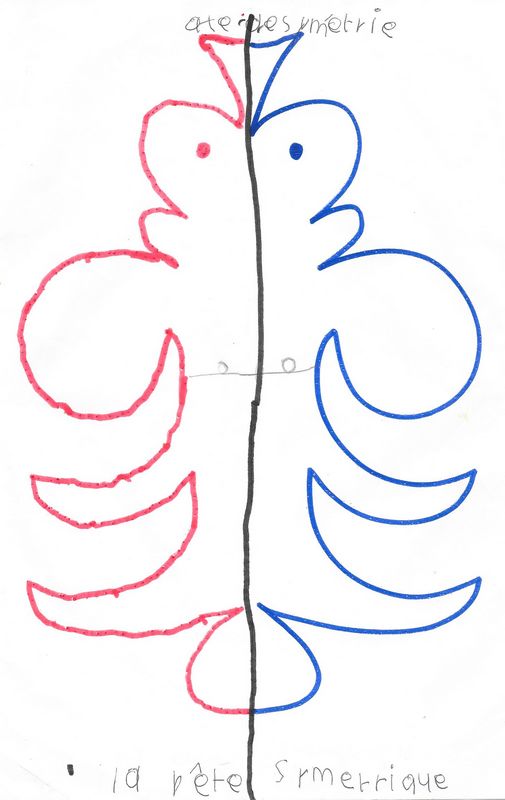

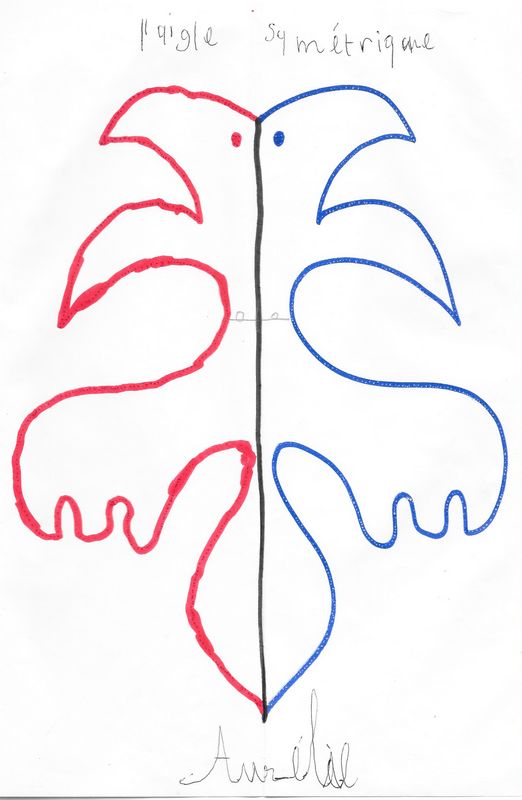
Peu à peu, on passe à l’idée que de vrais animaux ou vrais objets peuvent posséder un axe de symétrie.
Le premier exemple « réel » trouvé est l’enfant (Bertrand dans ce cas). On montre l’axe. Des correspondances : œil -œil, bras-bras, main-main, sont vérifiées …
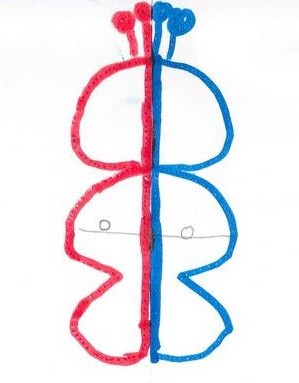
Puis on se déplace dans la classe à la recherche d’objets ayant un axe de symétrie.
Un bonhomme sur une peinture, puis une étagère, une autre étagère, la fenêtre. Les correspondances sont constatées.
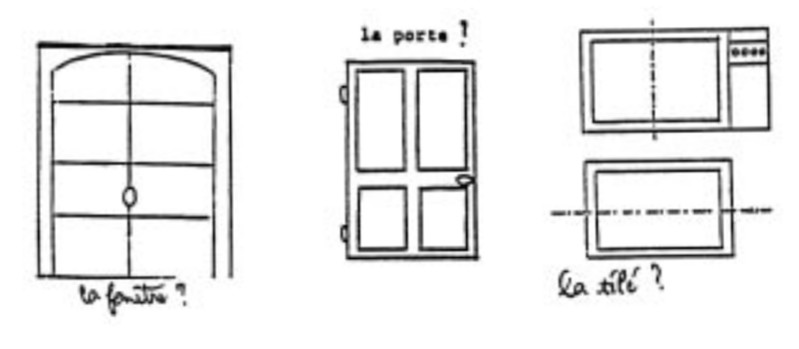
La porte ? La poignée pose problème, mais aussi les gonds. Il faudrait deux poignées et quatre gonds. Et encore la petite armoire et la télé.
Sans les boutons, rien que l’écran, la télé ça irait. Bertrand : « On peut mettre la main comme ça. » On a découvert un deuxième axe de symétrie !
Y-t-il d’autres objets avec deux axes ?
Oui : le tableau et une partie de l’estrade.
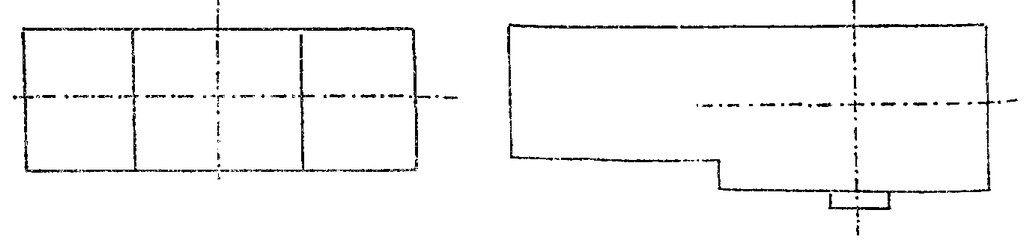
Et la bassine qui est là sur l’estrade et qui sert à mouiller l’éponge ?
Oui, il y en a tout plein ! Comme une roue de vélo !
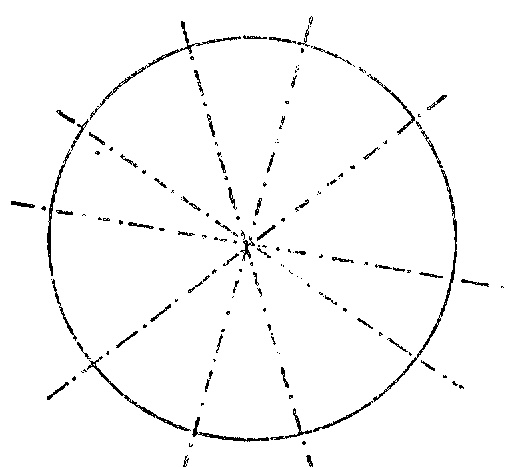
Une autre machine est découverte par hasard : le pliage découpage.
Certains, avec la technique pliage-pointe, faisaient tellement de perforations que finalement la partie centrale se détachait presque d’elle-même !
Et de ce fait, on s’est dit que ce serait plus rapide de plier puis de couper avec les ciseaux plutôt que de faire les trous.

De nombreux essais ont été testés. Le pli fait en dehors de la figure elle-même amène de nouvelles situations.


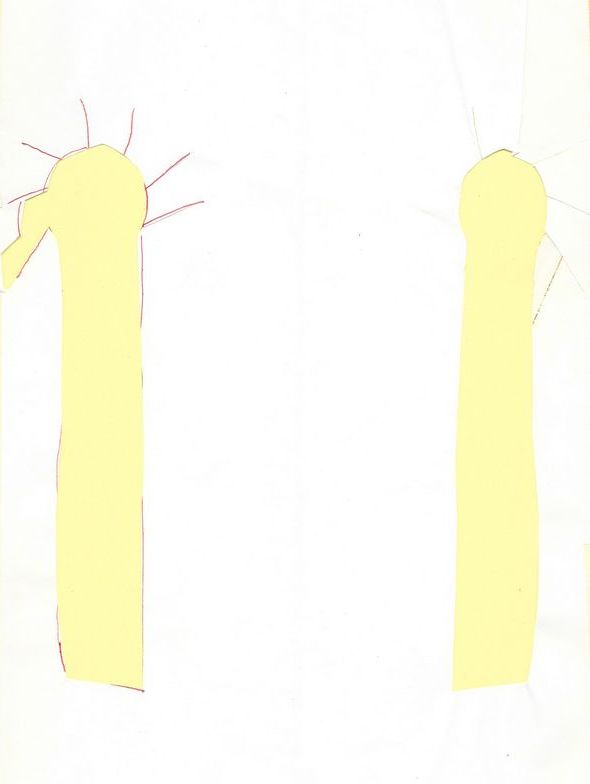



La technique pli-pointé, malgré tout plus facile à manier, est réutilisée lors de nombreux exemples.


La recherche libre se développe dans une alternance entre un travail individuel, des présentations à un groupe et des aller-retour entre le chercheur et l’adulte qui, dans ces tête à tête, doit s’assurer d’une communication la meilleure possible (écoute active, facilitation, empathie…).
Cette situation n’est pas sans rappeler la maman avec son bébé qui apprend à parler : les premiers gazouillis accueillis chaleureusement et renvoyés comme des réussites… « Il sait dire maman ! »
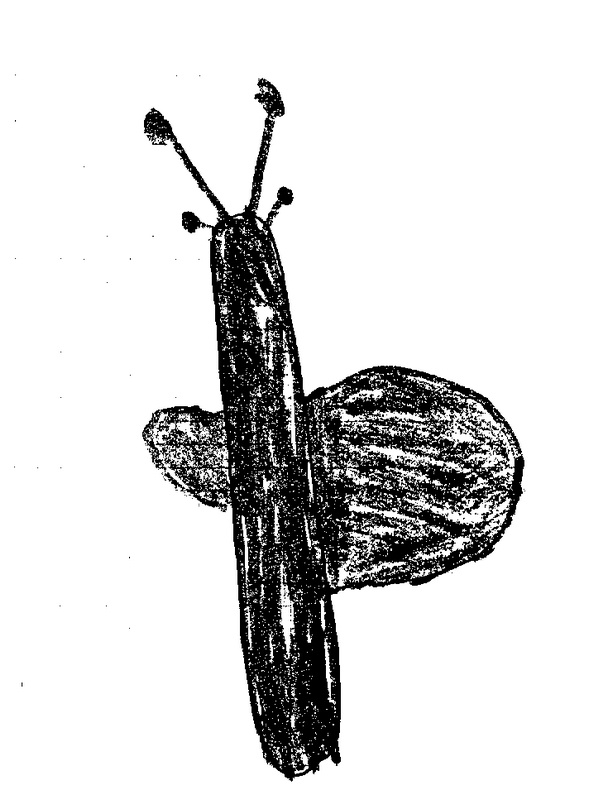
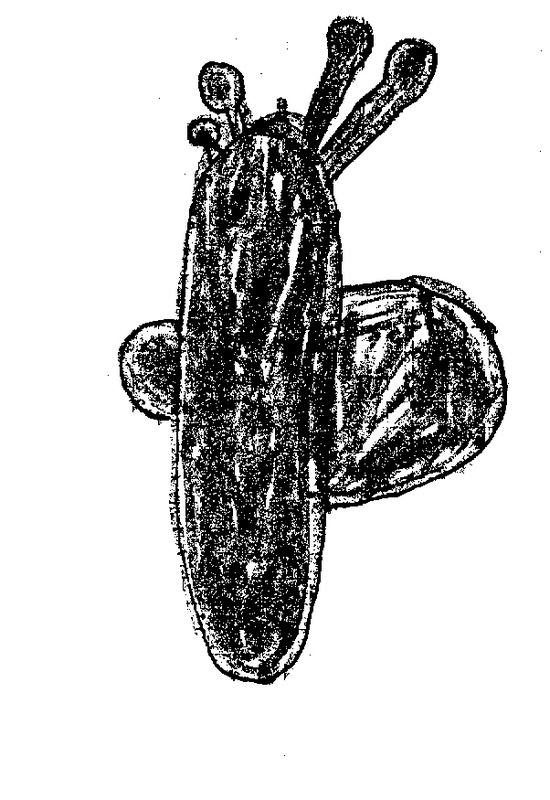
Les exemples ci-contre attirent particulièrement l’attention sur les problèmes d’orientation : la branche avec les feuilles, le crayon. Les pointes sont rapprochées, les bouts éloignés.
Peu à peu, après de nombreux tâtonnements par le dessin ou en s’aidant d’une machine, les premiers invariants se « conscientisent ». Avec les deux doigts écartés, Michaël me montre que les distances entre pointes de stylos et axe de symétrie sont les mêmes. Même chose pour l’autre extrémité. Et il renouvelle sa remarque pour d’autres exemples. Il symbolise cela par ![]() .
.
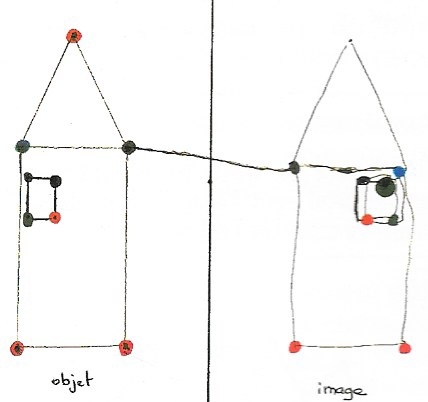
Ce premier invariant découvert va être utilisé pour s’affranchir peu à peu de la machine. Je lui propose une maison objet, à lui de dessiner l’image sans pliage-pointe. Les deux doigts qui montrent l’égalité des distances peuvent bouger pendant « le transport ». On décide donc de prendre une bande de papier, de noter la grandeur et de la reporter.
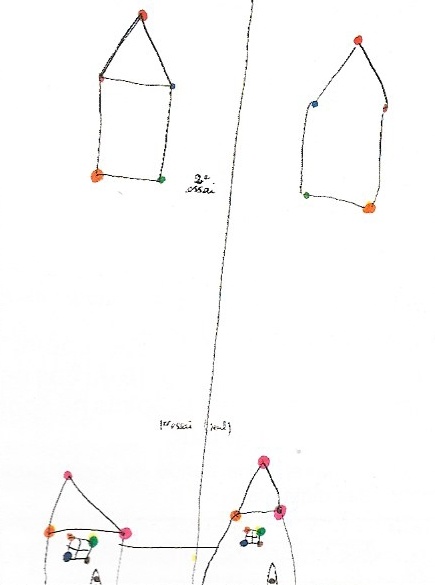
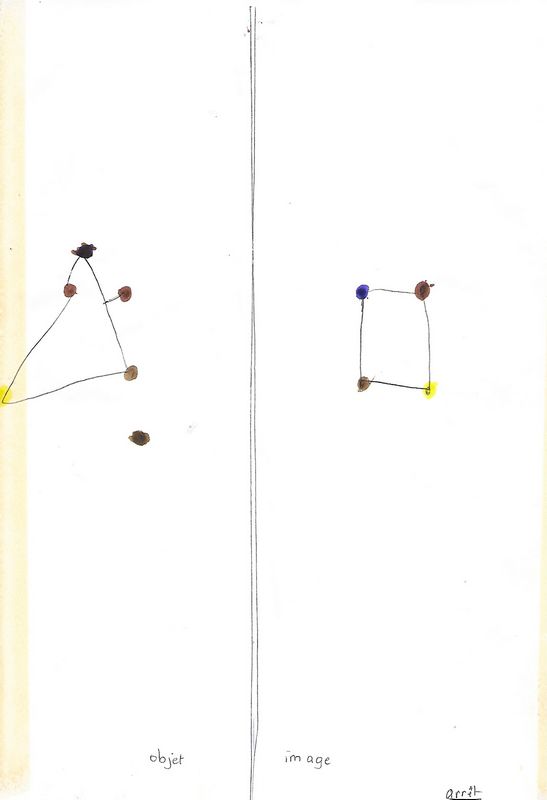
Michaël travaille seul et décide de l’objet : une maison. Un premier essai (en bas de la feuille) montre qu’il a plus confiance dans le dessin que dans sa nouvelle technique. La symétrie n’a pas encore son statut de transformation ponctuelle. Deuxième essai (en haut) avec moi. Après discussion, il s’avère que certains points sont stratégiques pour obtenir l’image. (On admet ici que l’image d’un segment est un segment. En effet, l’image d’un toit, c’est un toit).
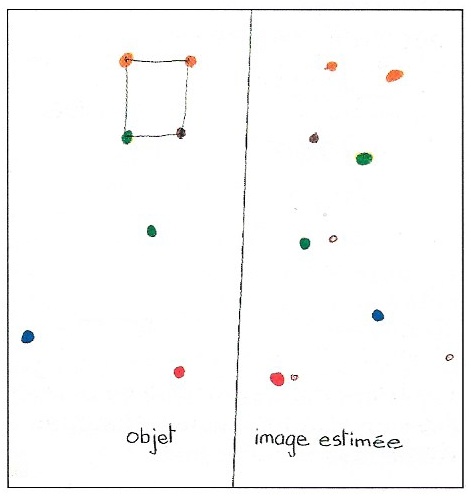
Il se donne une figure avec ses quatre sommets. Puis je lui propose trois points et lui demande d’estimer la position de leur image, puis de vérifier avec le pliage-pointe et enfin avec le papier (les distances).
Nouvelles tentatives.
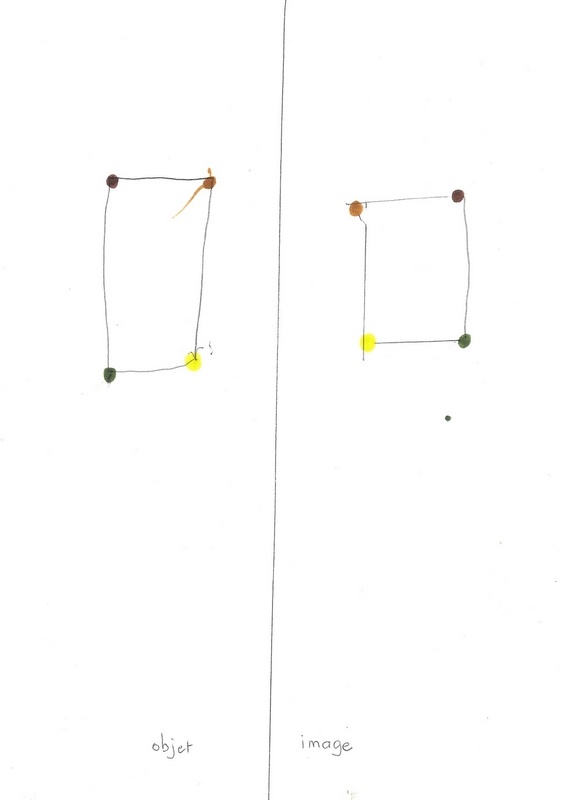
Pour celle de gauche, l’invariant de l’équidistance par rapport à l’axe semble fonctionner : il y a bien l’effet miroir.
Mais la deuxième lui pose vraiment problème : les choix du triangle comme objet (sans doute un peu téméraire) et des points caractéristiques ont un peu corsé l’affaire …
Ces deux productions sont les dernières de cette série. Mickaël décide de s’arrêter et de passer à une autre recherche. Il en a plusieurs en cours simultanément.
Le texte libre d’un enfant déclenche un intérêt pour un événement particulier : le drôle de papa. Des propositions de « drôles de … » sont faites par le groupe, puis reprises individuellement par Mickaël. C’est une phase de sensibilisation au phénomène avec une première emprise sur l’événement qui se traduit par des essais de reproduction par le dessin plus ou moins satisfaisants.
Peu à peu une exigence s’impose : il faut être capable de produire un objet symétrique correct. L’objet de la recherche se précise.
Une première présentation au groupe engage le chercheur dans la découverte du moyen de reproduction du phénomène le plus fidèle et efficace possibles.