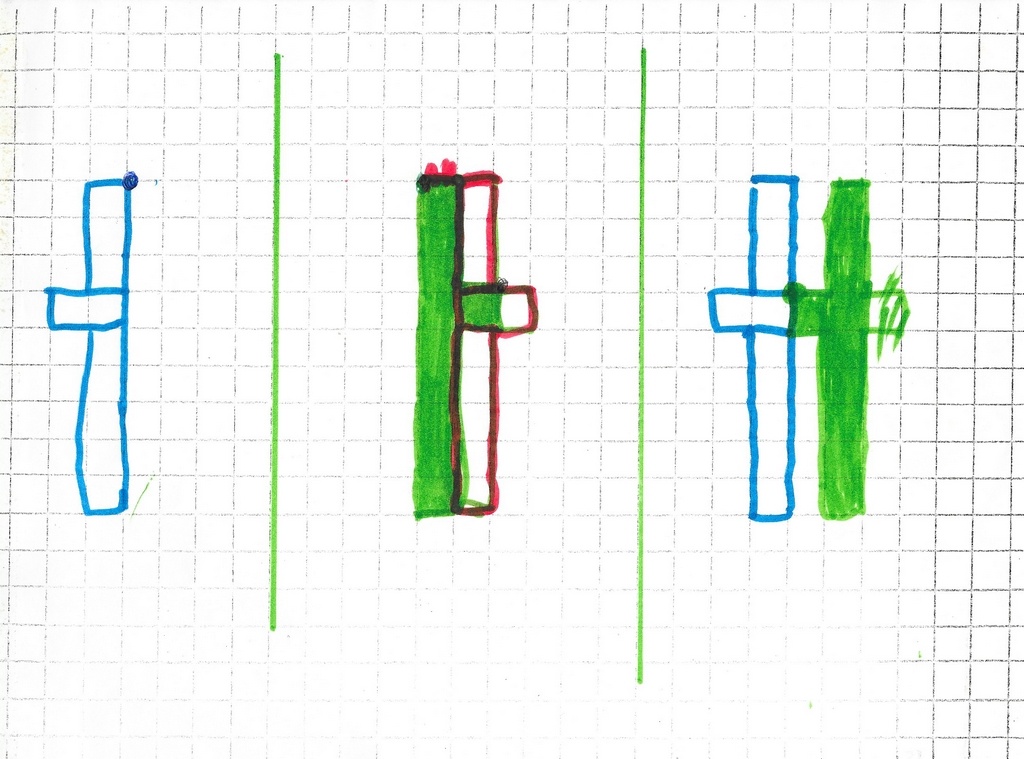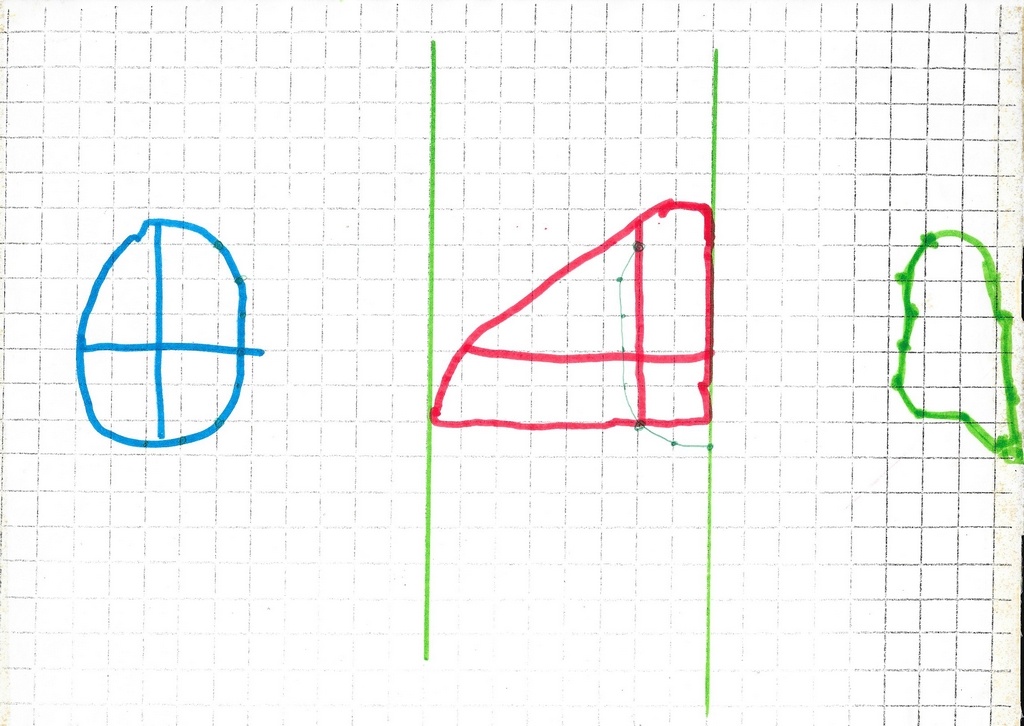Le contenu de la page
6. suite de la recherche
7. prolongements
école : classe unique (section enfantine, cycle 2 et 3 : enfants de 5 à 11 ans
niveau concerné : cycle 2
recherche individuelle : Mickaël, entre 5 ans 1/2 et 8 ans.
domaines : géométrie de transformation, symétrie axiale, loi de composition
connexions : invariance, angle droit, distance, alignement, explorations verticale ou horizontale, vecteurs
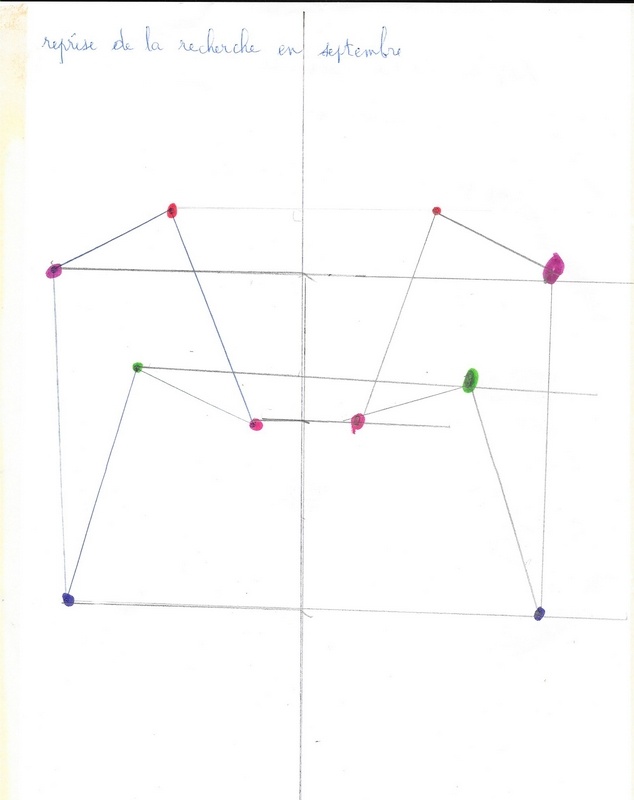
Reprise de la recherche : composition de symétries
Mickaël reprend la recherche à la rentrée de septembre. Il est maintenant en CE1 (7 ans).
On se remet dans le bain…
Quelques exemples pour se rappeler du « mode d’emploi »
Mais il se souvient de ma remarque, lors de sa présentation avant les vacances, sur ce que font les grands. Il se lance donc dans la composition de deux symétries axiales…
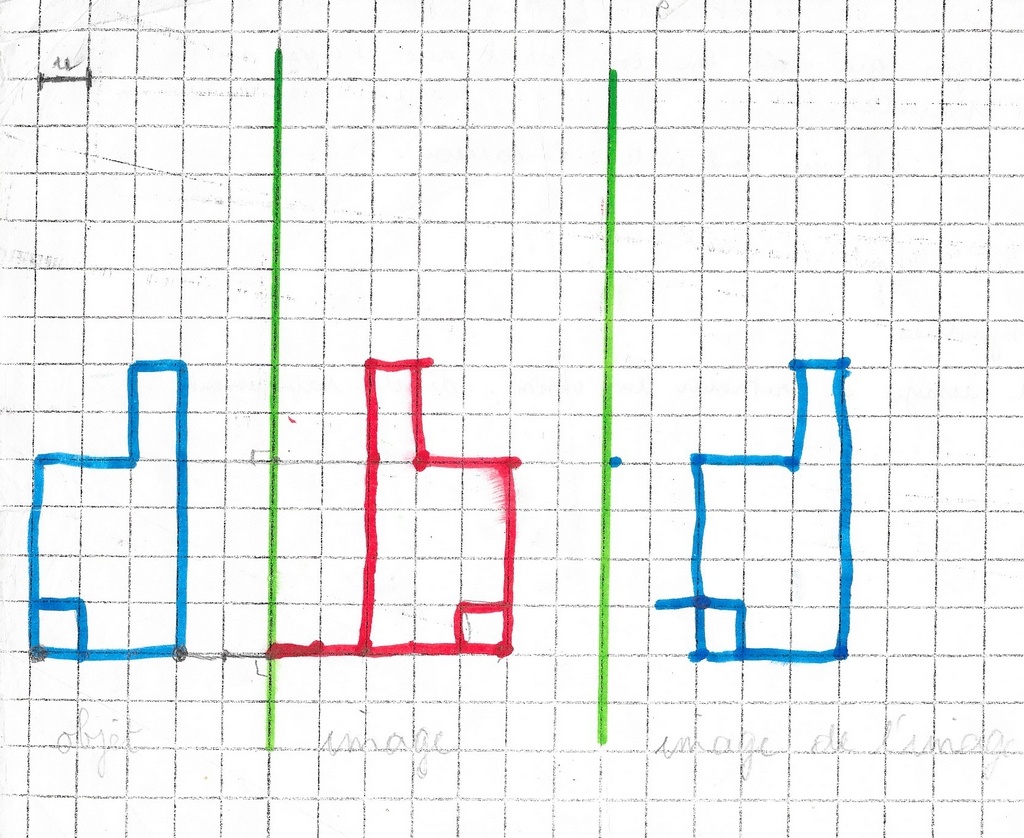
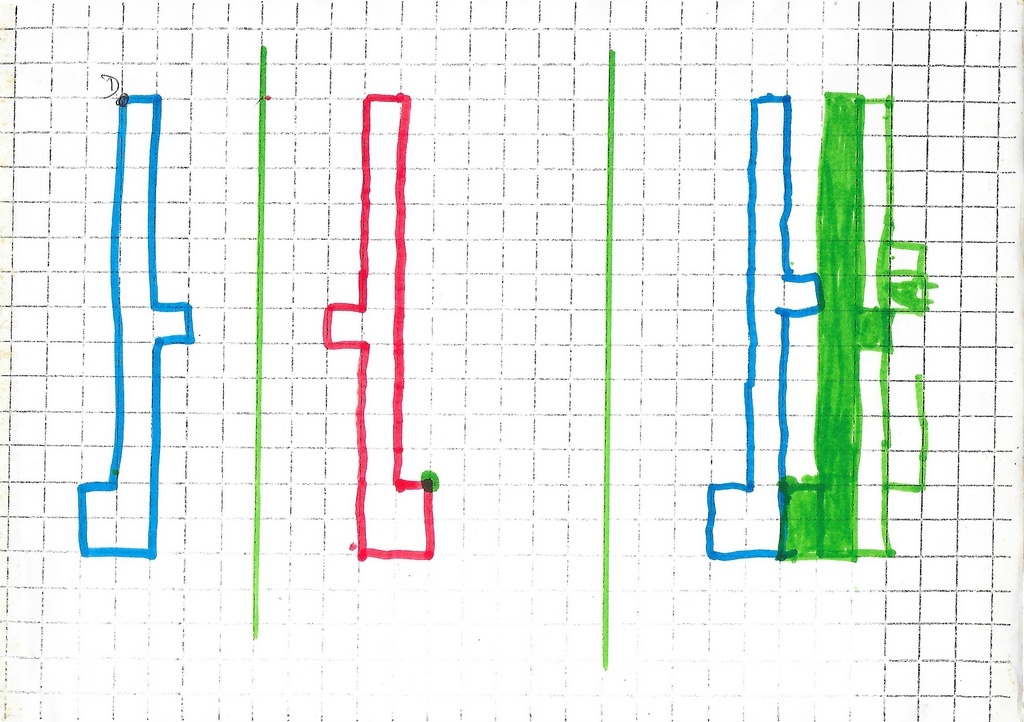
Et démarre avec ma proposition : un objet bleu et deux axes.
La couleur du produit final (rouge d’abord puis bleu) montre qu’il a hésité sur son statut : rouge en tant qu’image d’un objet ou bleu pour sa similarité avec l’objet initial : image de l’image).
La tentative du bas était condamnée par la position de l’objet initial choisie.
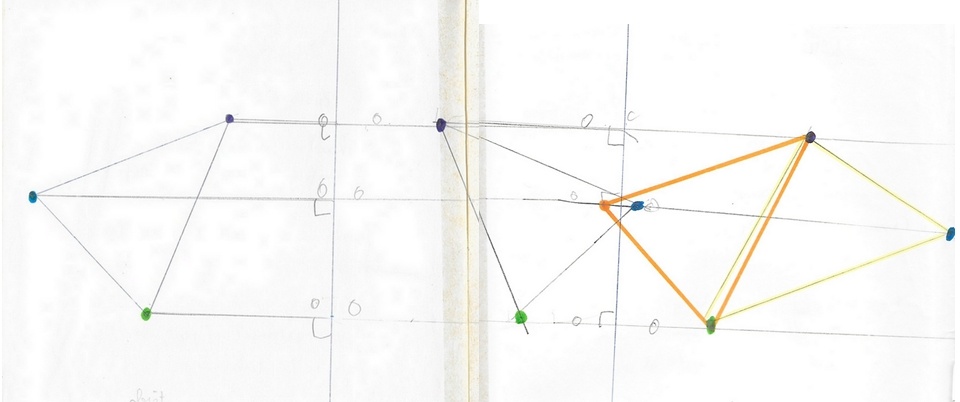
Le triangle objet est à gauche (points bleu, vert, violet). La grande marque jaunâtre verticale est la trace du scotch qui relie deux feuilles du dépliant.
Mickaël utilise bien la technique, sauf pour l’image de l’image du point bleu qui le met en difficulté. Il est vrai que le choix (mon choix) malencontreux du 2e axe ne l’aide pas… Le 2e axe est trop proche du premier, ce qui ajoute une difficulté supplémentaire: l’image et l’image de l’image se chevauchent. Il n’envisage pas que cette image puisse être ailleurs qu’à droite du 2e axe. Il la place donc dans cette zone, à la distance entre le point bleu objet et l’axe 1.
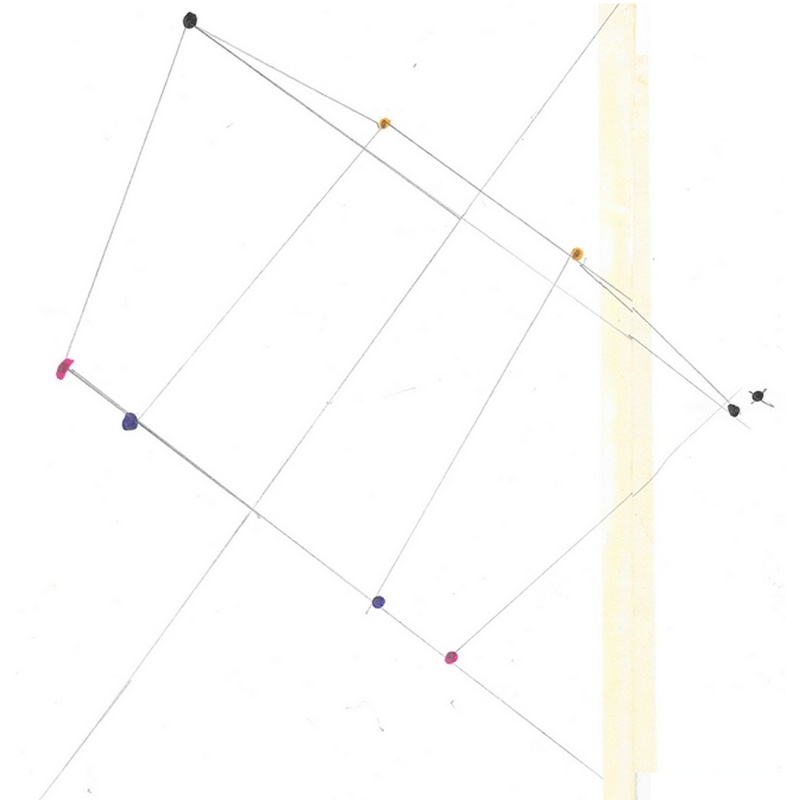
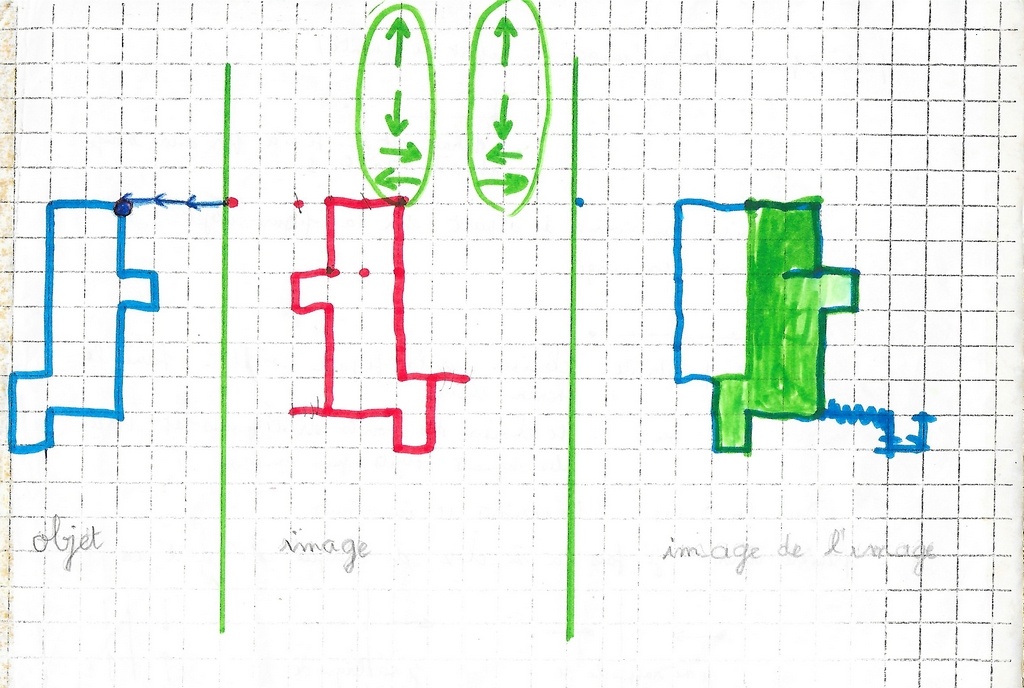
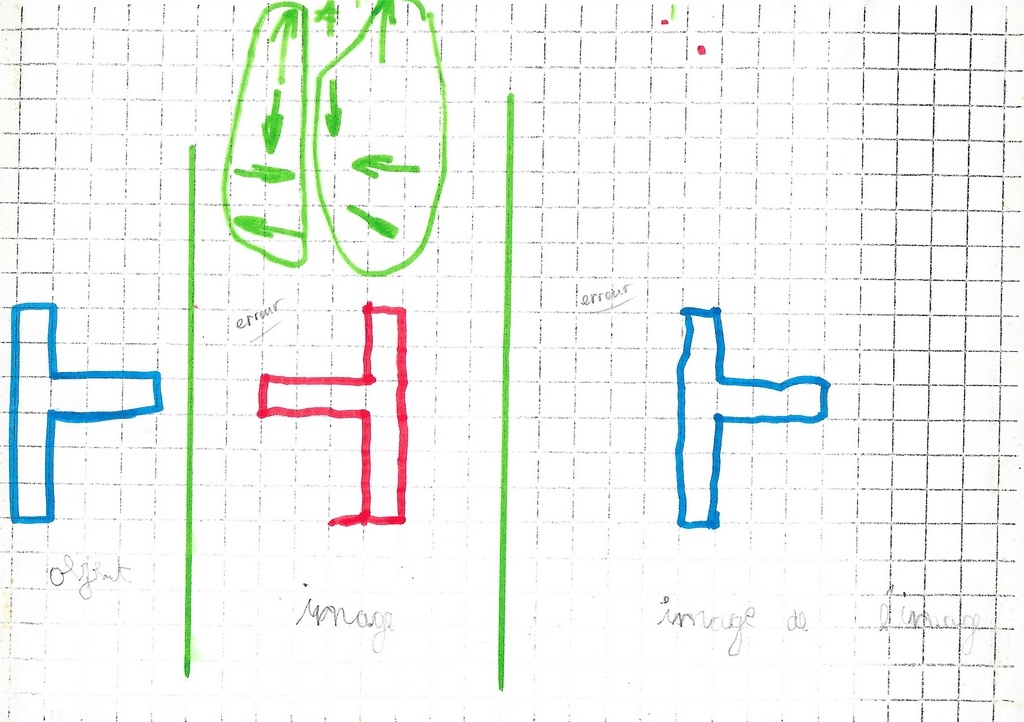
Mickaël vient me voir me voir.
L’image de l’image (en jaune) produite ne le choque pas. La « vision » qu’il avait précédemment s’est émoussée. (Peut-être à cause de la technique relativement lourde à cet âge.)
Après analyse de la production (devenir de chaque point), le triangle orange rectificatif est tracé.
Un nouvel outil d’exploration performant
Étant donné que l’objet de la recherche porte maintenant sur la composition de symétries (« Qu’est-ce que ça donne si je compose deux symétries axiales (avec axes parallèles)»), la technique de production d’images symétriques risque très vite de devenir par sa complexité un obstacle.
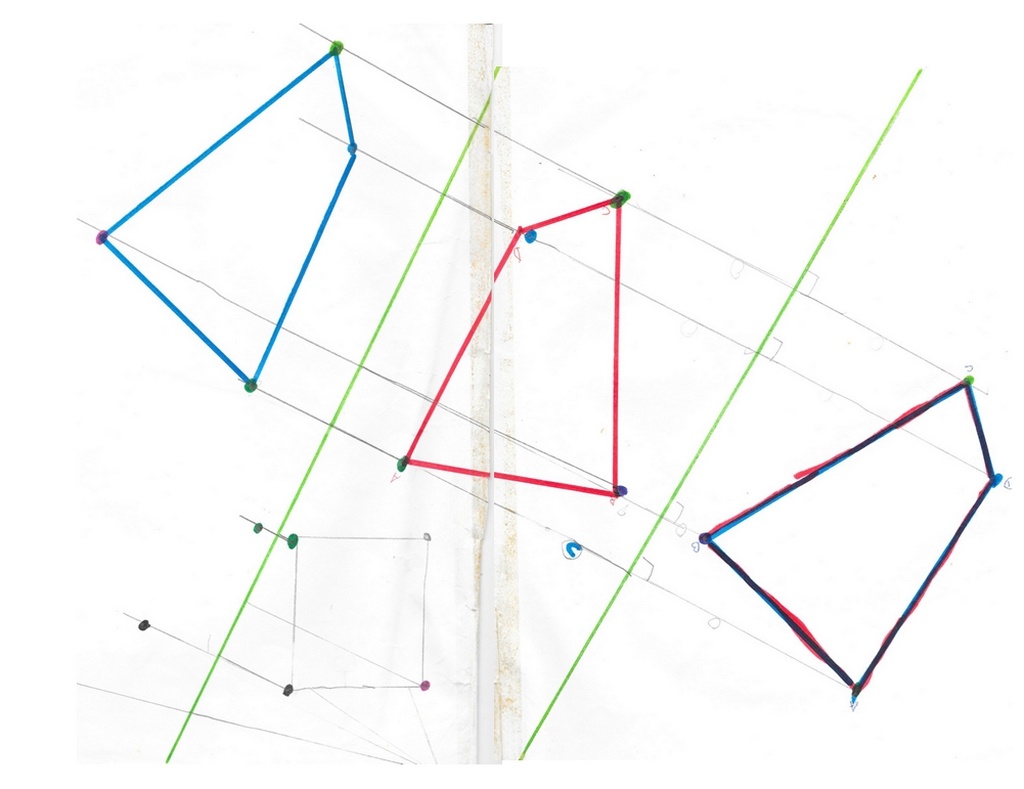
Je propose donc une feuille quadrillée à Mickaël. On en voit l’intérêt ensemble :
– les lignes qui font des coins droits avec des axes de symétrie verticaux sont déjà présentes ;
– pour les distances, on peut utiliser les carreaux comme unité à la place de la bande de papier.
On refait deux symétries pour retrouver la « vision » qui permet de détecter rapidement l’erreur éventuelle.
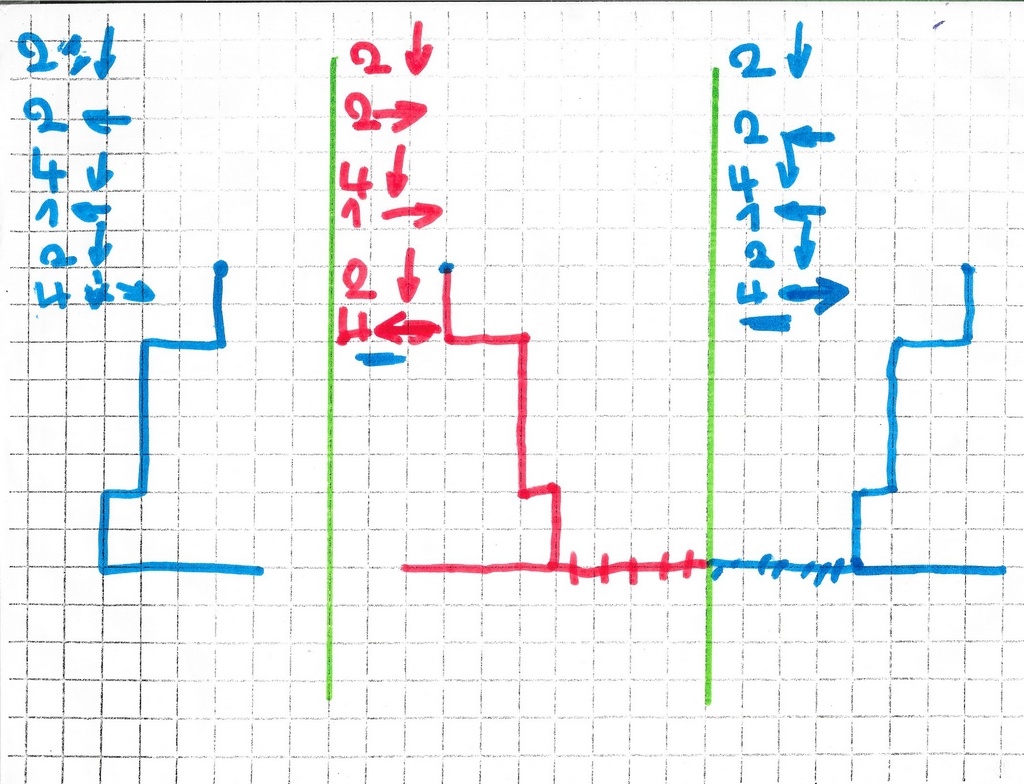
Manifestement, l’utilisation de la « machine » quadrillage n’est pas évidente.
Le premier problème qui se pose est le report de l’unité dans les déplacements : Mickaël se choisit un point sur la figure objet, puis cherche son image. Pour cela, il commence à se diriger vers l’axe de symétrie. Mais avant le moindre mouvement, il dit « un ». Et logiquement, après le premier pas, il dit « deux ». Au lieu de compter les intervalles, il compte les bornes.
Nouvelle tentative à côté de moi. La tactique qu’il adopte est de choisir un point de départ sur la figure objet vue comme un chemin, de trouver son image, puis essayer de reproduire le chemin image : 3 unités de l’axe jusqu’au point. Puis 3 unités de l’axe mais dans la direction opposée.
Puis il commence à dessiner le chemin image : intuitivement, ça descend du côté bleu, donc il faut descendre du côté rouge : 2 unités vers le bas. Puis 1 u vers la gauche qui se traduit par …. hésitation. On reconvoque l’équidistance à l’axe, et donc c’est à gauche qu’il faut aller. Après pas mal de réflexion, le chemin image est tracé et les lois de changements de déplacement sont inscrites :
– 1 unité reste 1 unité, donc n unités restent n unités ;
– pour les directions : en haut et en bas ne changent pas, gauche et droite changent.
Une autre vision : je fais « la même chose » de chaque côté de l’axe :
– si je me rapproche de l’axe côté objet, je me rapproche de l’axe côté image
– si je descends ou je monte, alors je descends ou je monte.
Suivent de très nombreux essais, dont certains très téméraires. Les images revues sont en vert.
On assiste là à un changement de stratégie dans l’exploration de la transformation. Jusqu’à présent, Michaël se choisissait des points stratégiques objets, puis « calculait » leurs images respectives en utilisant les invariants (coin droit, égalités des distances) de la symétrie découverts et traçait enfin la figure image (en admettant que l’image d’un segment est un segment).
En s’intéressant au devenir des points du chemin objet, il optait pour une exploration « horizontale ».
Maintenant, le quadrillage semble l’inciter à utiliser une autre procédure : Mickaël se choisit un chemin objet et son point de départ, cherche l’image du départ, puis applique les règles des directions et l’invariance des longueurs pour tracer le chemin image. On peut qualifier cette exploration de « verticale ».
C’est l’idée très générale de « désobéissance » qui opère : à l’aide d’un mode d’emploi (déplacements, point de départ, unité de déplacement …), on se propose de tracer une figure dans le monde « objet », puis on reproduit à nouveau cette figure dans le monde image en respectant ou pas les règles du mode d’emploi initial. C’est cette « désobéissance » qu’il s’agit d’explorer.
C’est cette désobéissance qui servira aussi de moteur d’exploration dans le domaine des fonctions, numériques ou pas, et de la découverte de techniques opératoires.
De nombreuses tentatives montrent que Michaël maîtrise correctement les changements de directions, mais plus difficilement les reports de distances.
On décide donc de bien faire attention aux points de départ et à noter les déplacements, et leurs transformés.
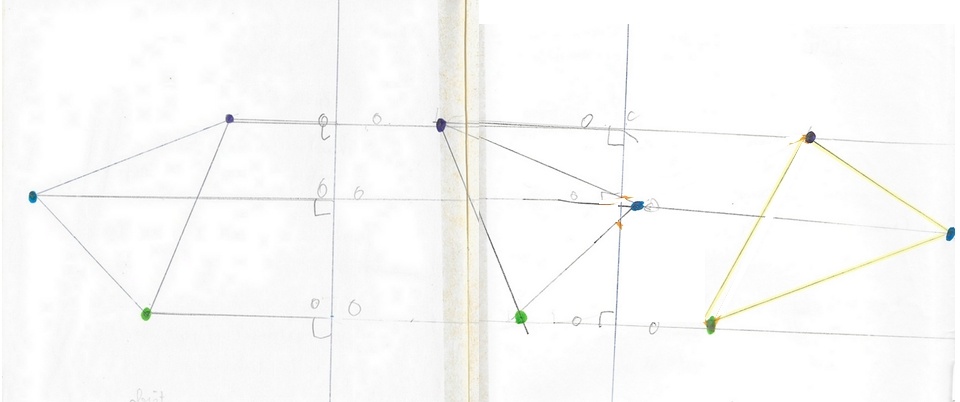
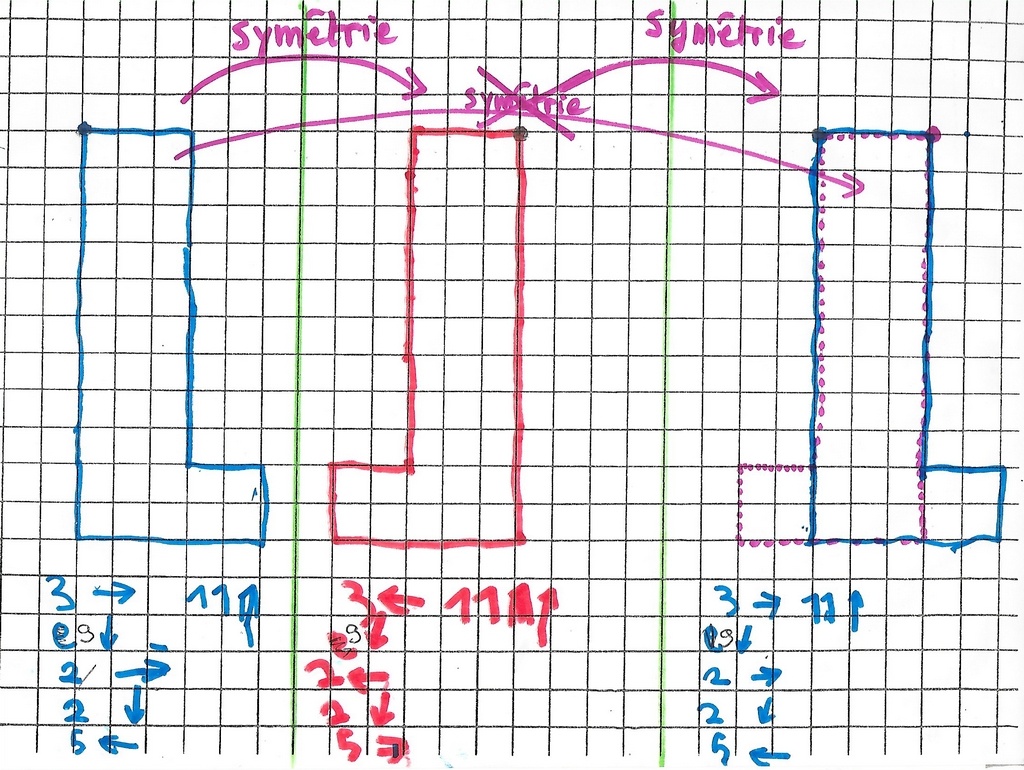
Tout au long des nombreux essais, certaines constantes apparaissent :
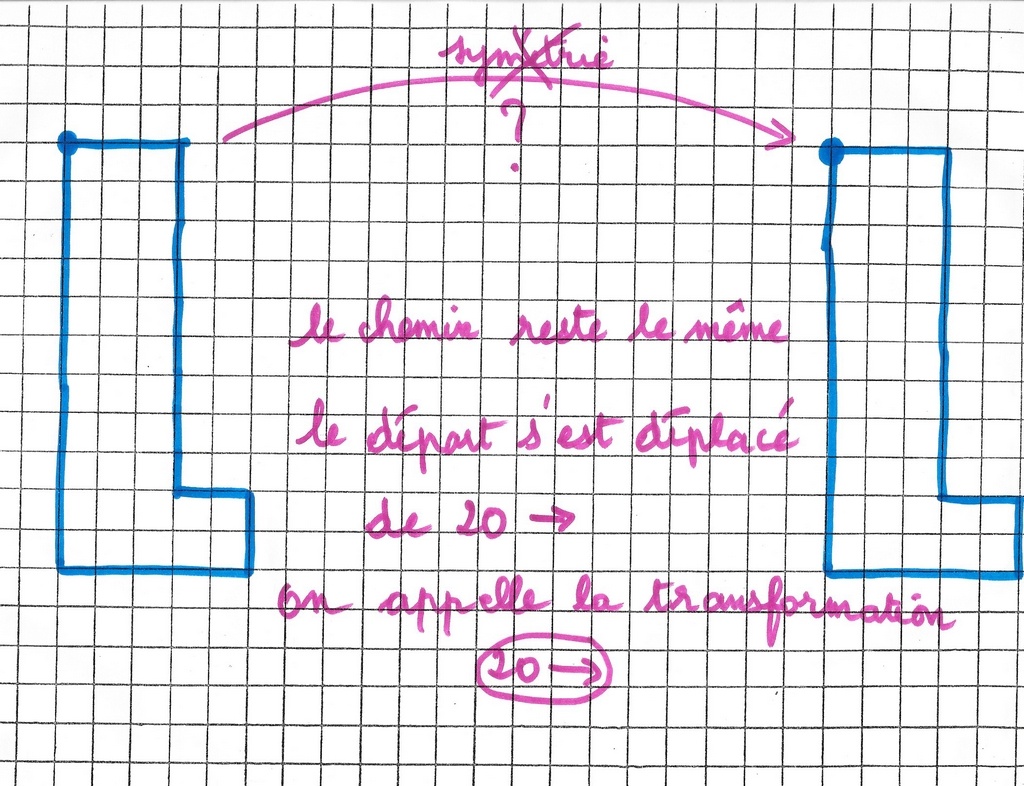
– le chemin image de l’image que l’on appellera composé est identique au chemin objet ;
– les codages de chemins sont aussi les mêmes ;
– mais le point de départ a changé.
Je ne passe pas de l’objet à l’image de l’image par une symétrie ! Pour nous en convaincre, on a tracé en pointillés rouges la symétrique de l’objet
Quelle est cette transformation nouvelle ?
Elle conserve le chemin, mais le point de départ s’est déplacé de 20 –>.
Nous l’appelons la transformation 
Plusieurs questions se posent :
– Est-ce que c’est toujours vrai ? Est-ce que si je compose deux symétries (orthogonales avec axes parallèles), j’ai toujours une transformation composée comme –>20 ?
– Pourquoi 20 ?
– Comment fonctionne cette nouvelle transformation ?
Le bond est ici immense !! Le drôle de papa et le monde sensible se sont potentialisés (ce qui ne veut pas dire qu’ils sont effacés : ils peuvent s’actualiser si nécessaire). Les préoccupations ne portent plus sur un contexte précis mais sur des éléments qui eux sont totalement décontextualisés : les symétries, les compositions de symétries, les transformations composées… Mais aussi la vérité en mathématique, la preuve…
La symétrie axiale, dont la maîtrise était l’objet de la recherche initiale, devient avec la composition de transformations, simple élément d’une recherche d’un niveau d’abstraction plus élevé.