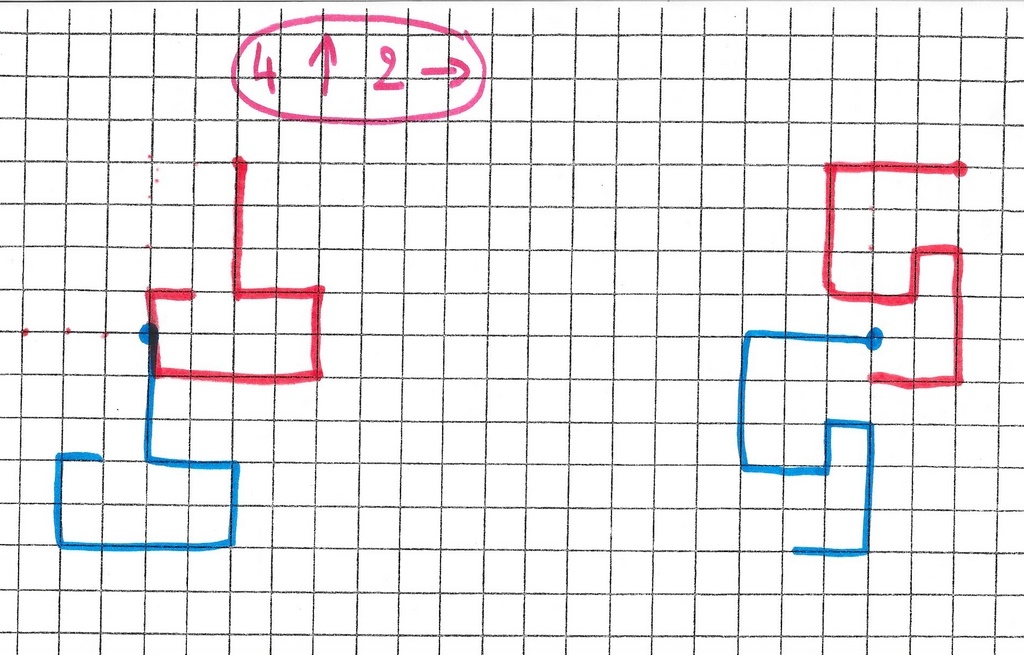Le contenu de la page
7. prolongements : la translation
école : classe unique (section enfantine, cycle 2 et 3 : enfants de 5 à 11 ans
niveau concerné : cycle 2
recherche individuelle : Mickaël, entre 5 ans 1/2 et 8 ans.
domaines : géométrie de transformation, loi de composition de symétries axiales, translation
connexions :exploration horizontale, vecteur

une nouvelle transformation
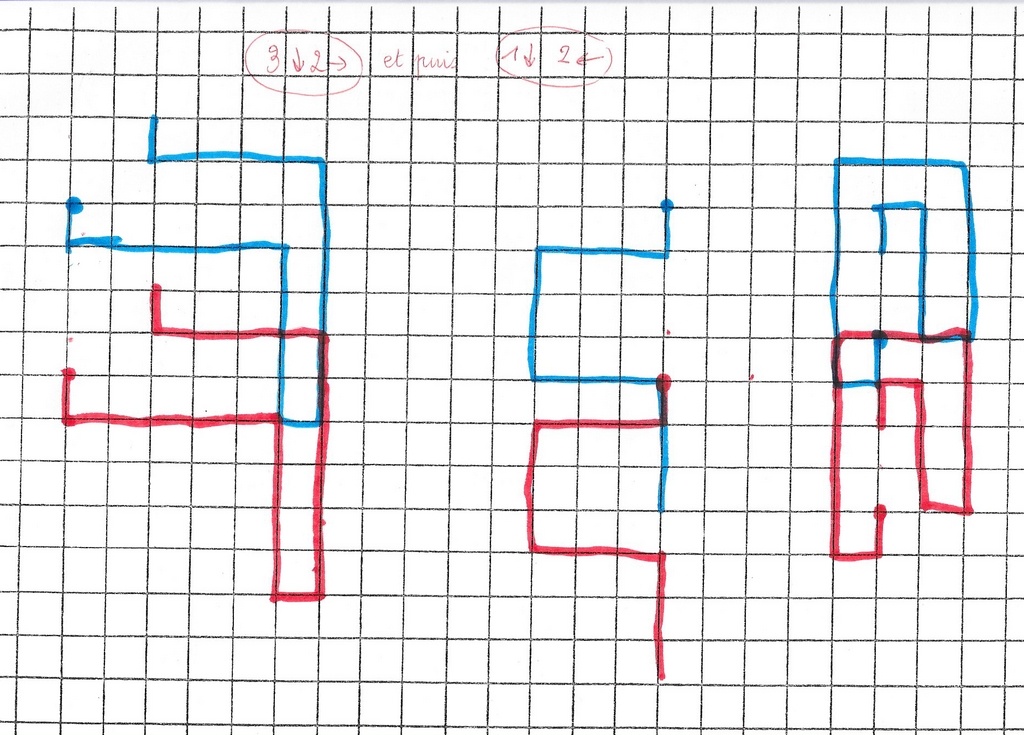
Mickaël part à la découverte de cette nouvelle transformation obtenue en composant une symétrie (axiale) avec une autre symétrie axiale. Il sait déjà que les chemins restent identiques, mais que le point de départ a changé de place.
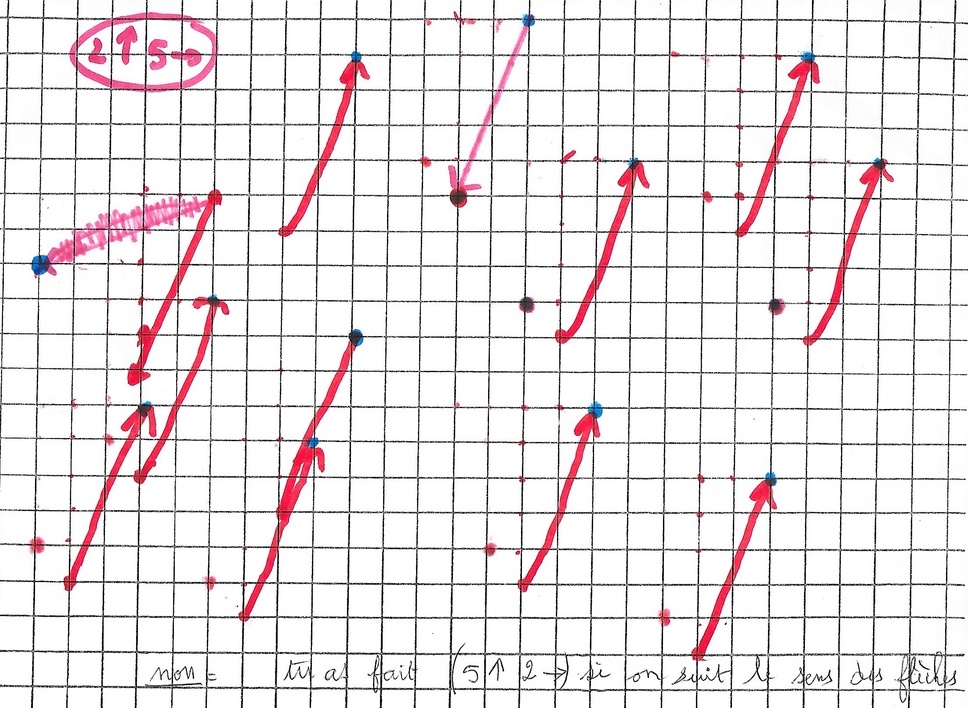
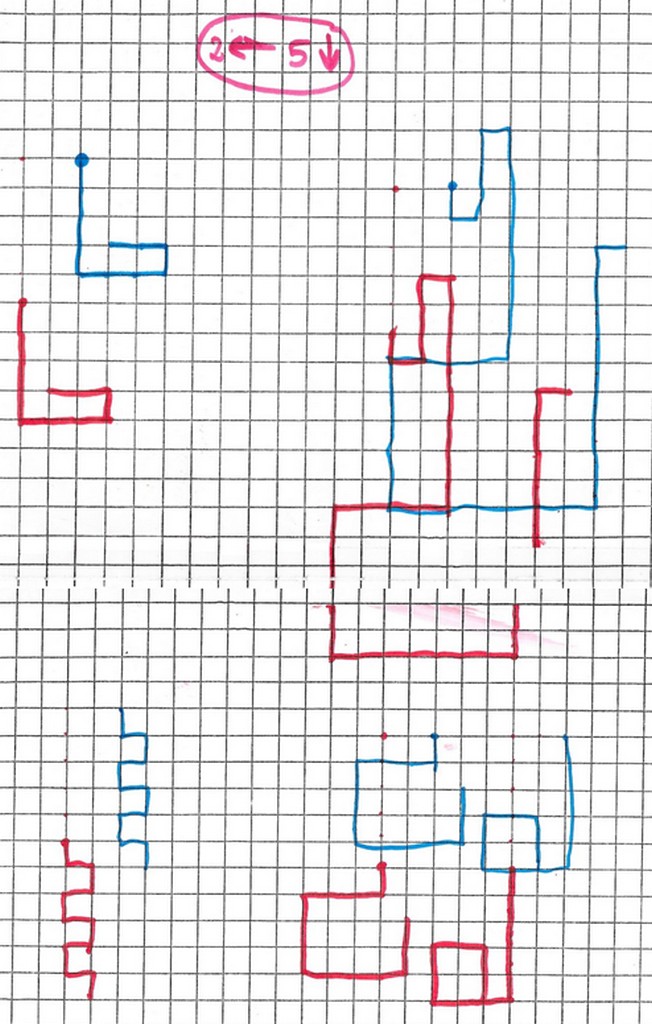
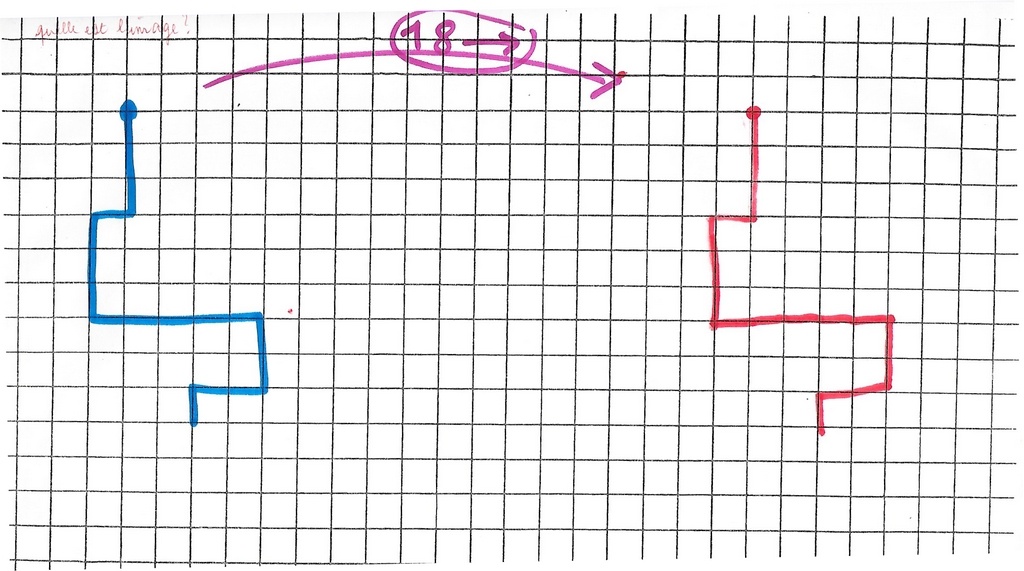
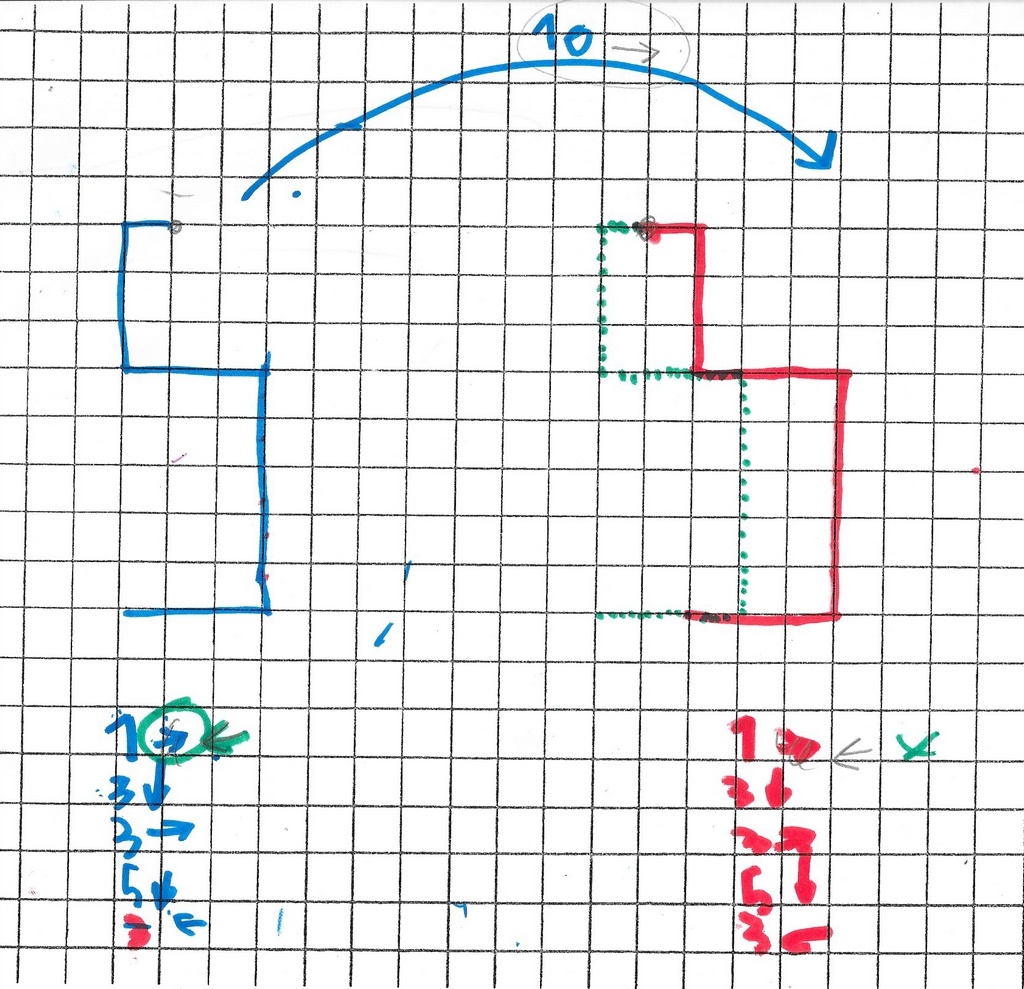
Il se choisit une transformation : 18–> et un chemin objet avec un point de départ, puis cherche le chemin image.
Il se choisit un chemin objet avec point de départ, puis positionne deux images du chemin au hasard sur le quadrillage.
Il cherche ensuite le nom des transformations.
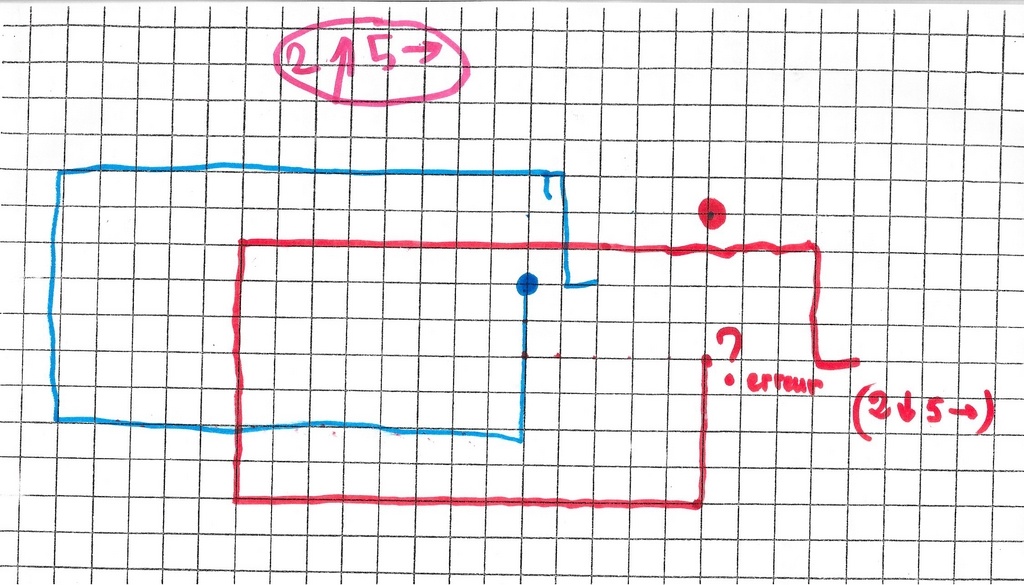
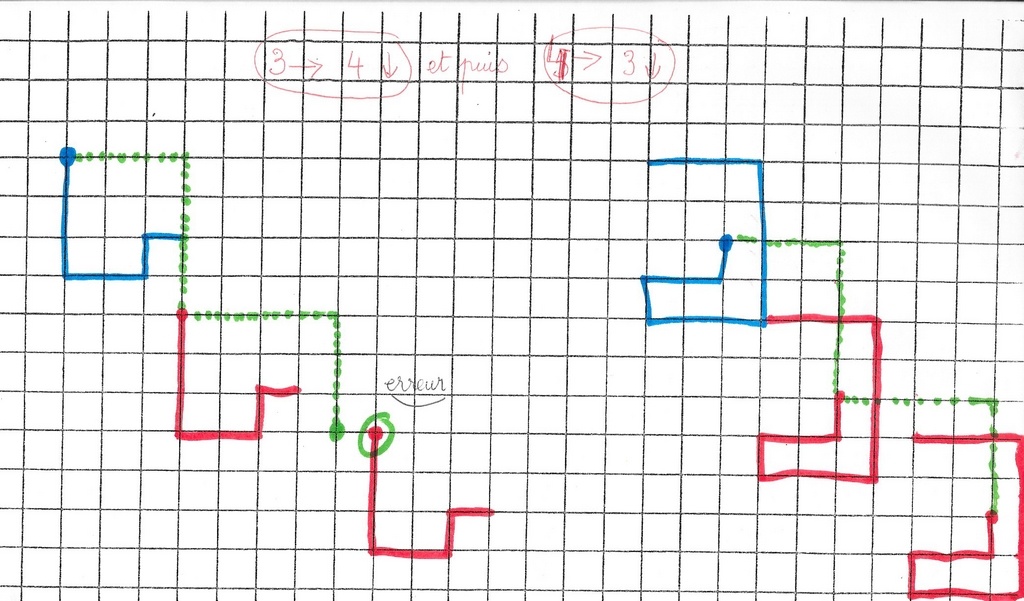
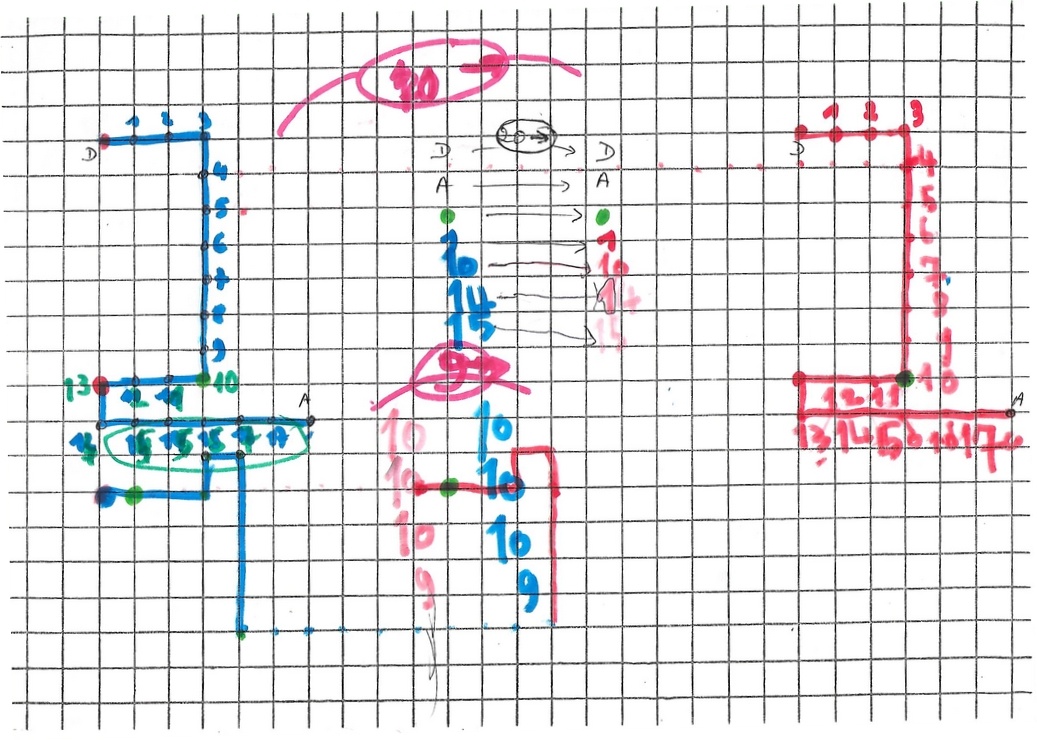
Une erreur dans le choix du point de départ image nous amène à nous pencher de plus près sur le devenir des points objets.
Au point de départ D correspond le point de départ image D, au point d’arrivée A le point image A, au point vert le point vert.
Chaque point image est à 20–> de son point objet.
Même remarques pour la transformation 9–>
En s’intéressant au devenir des points du chemin objet, Michaël quitte l’exploration « verticale » et revient à l’exploration « horizontale » des débuts.
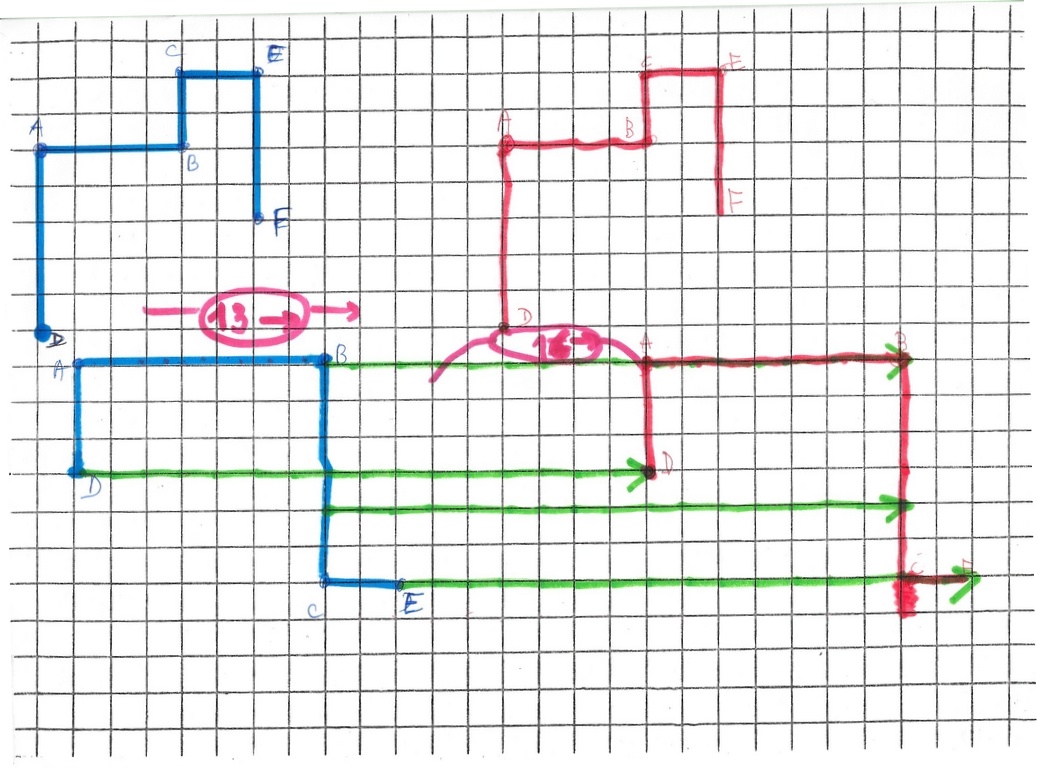
On travaille ensemble : je lui propose une figure objet avec les points de changement de direction nommés et une transformation : 13 –> . Je lui demande de s’intéresser aux points images correspondants comme il l’a fait précédemment.
Même constatation : le point A image est à 13–> de son point objet. Pareil pour les autres points.
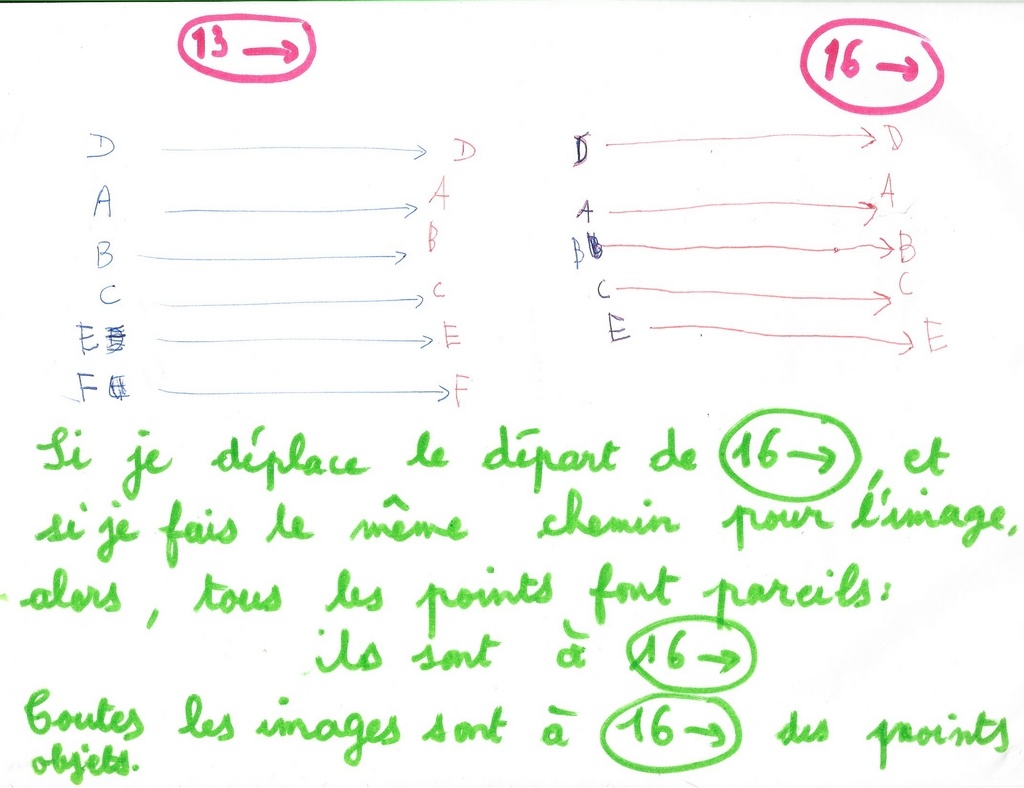
Deuxième exemple avec 16 —> .
A chaque fois, il me montre le « chemin » des points qu’il matérialise par une flèche verte.
Je note ses remarques :
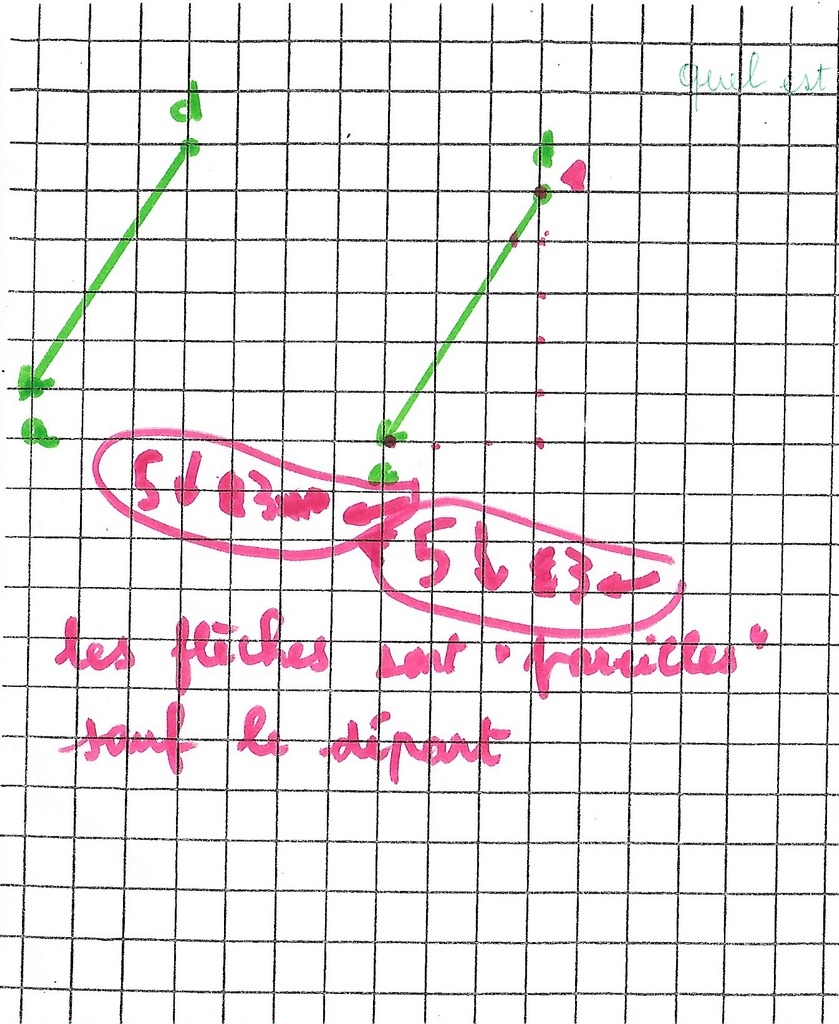
– Toutes les flèches mesurent 16 pas (unités) : tous les points images sont à 16 de leur objet.
– Les flèches sont parallèles. (Le parallélisme appartient au patrimoine commun mathématique de la classe).
– les flèches n’ont pas le même point de départ.
Moi : « On pourrait donner un nom à toutes ces flèches pareilles »
Mickaël : « On les appelle les flèches 16 —> »
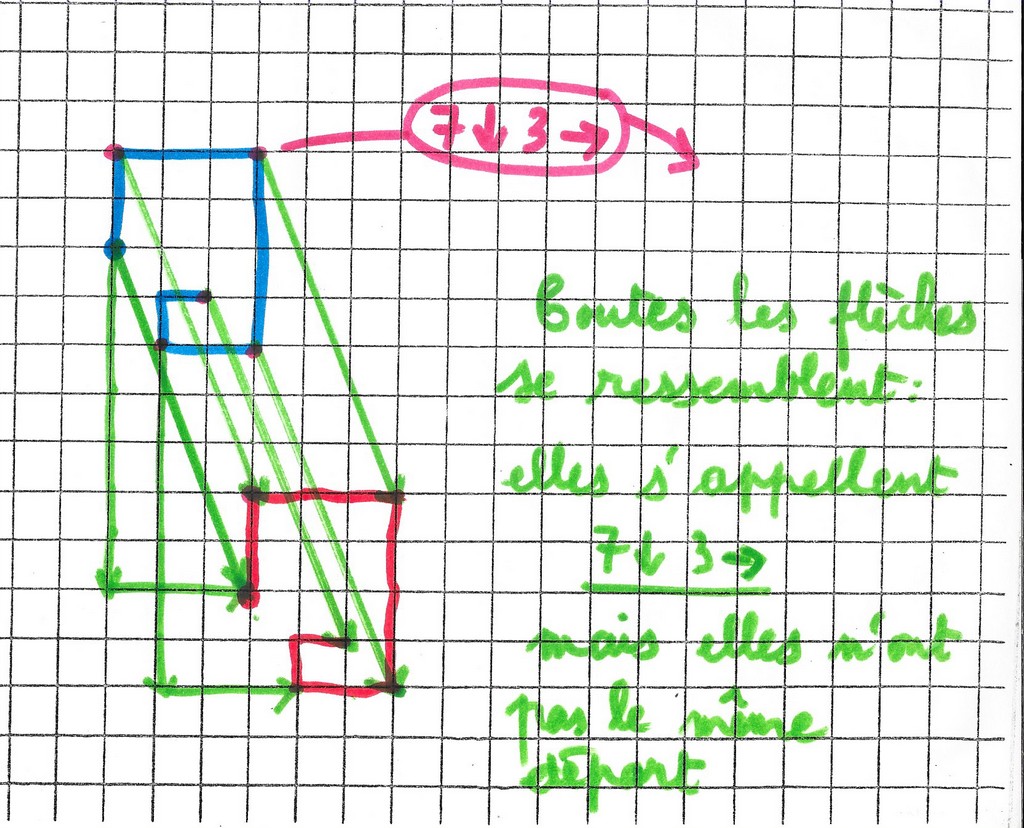
Une transformation un peu plus complexe ![]()
Michaël dessine les « chemins » qui transportent les points.
La flèche dd’ fait le même travail que
![]()

Il repart travailler seul.
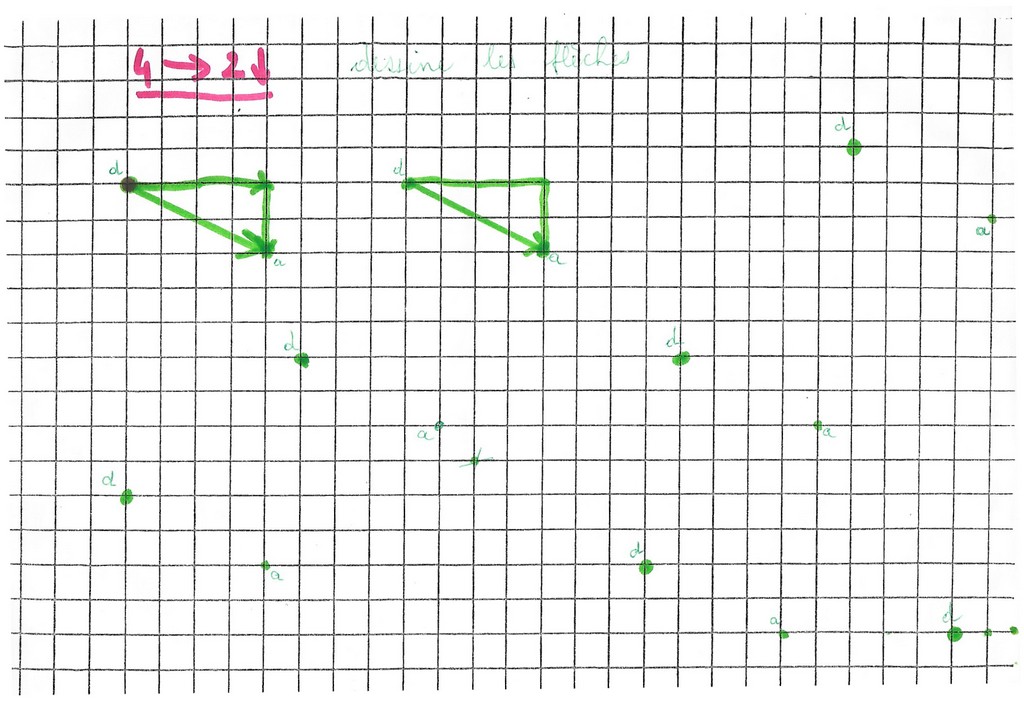
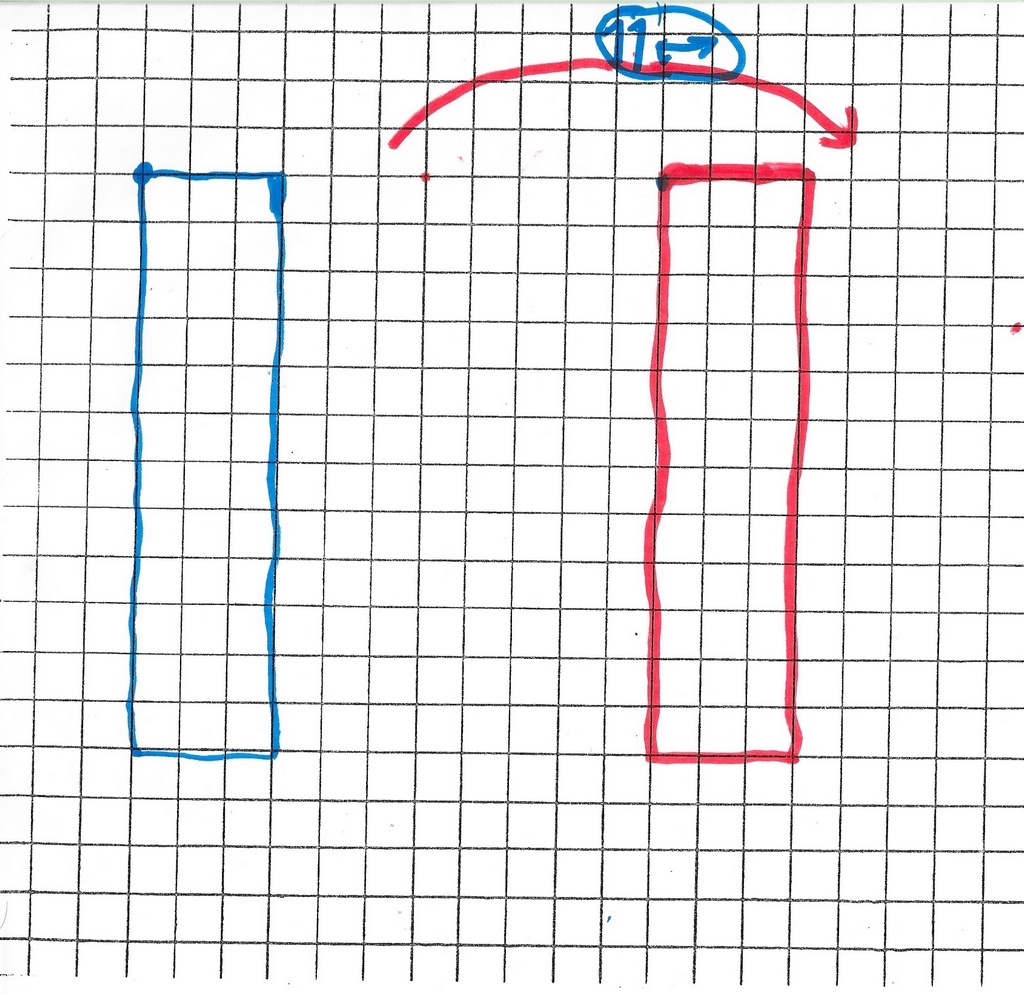
Il dessine une flèche entre deux points d et a, cherche le nom de la flèche, choisit un autre point de départ d puis exécute le code.
Il refait la même chose pour trouver une autre famille de flèches « pareilles ». Un intrus s’est glissé dans la famille (4 gauche, 4 bas). Mais comme il est très voisin, on ne le repère pas facilement.
De nombreux tâtonnements, essais, erreurs, réussites suivent.
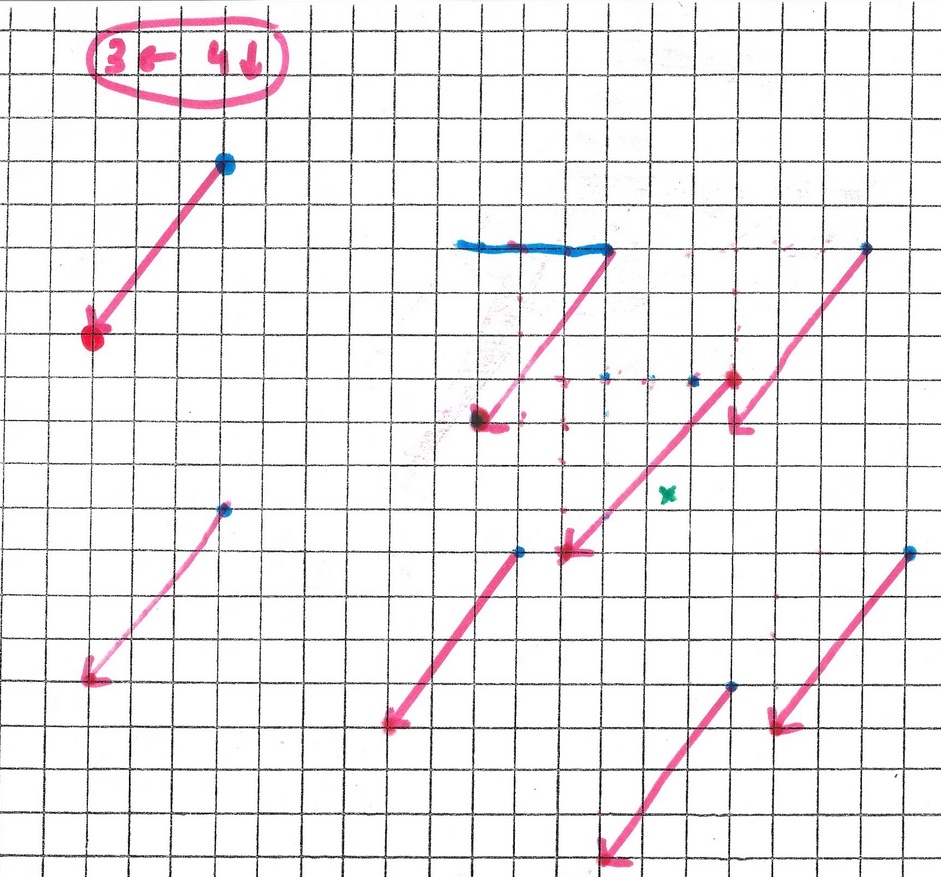
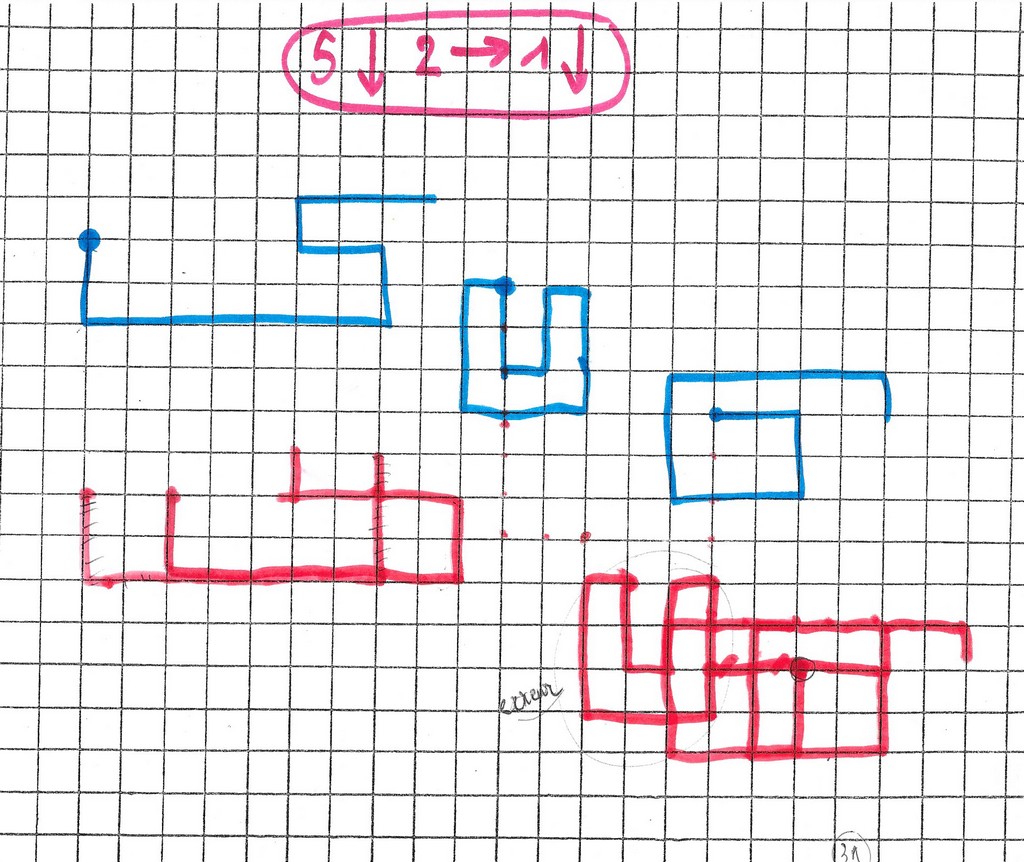
On revient à la transformation des chemins. (à droite)

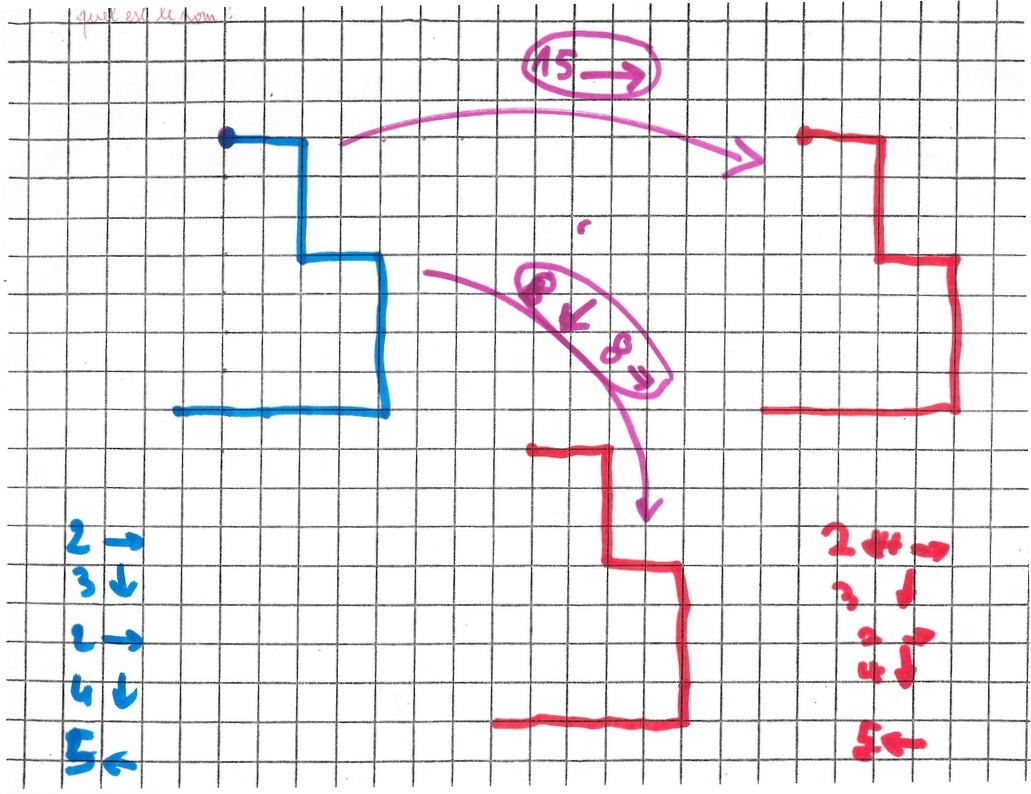
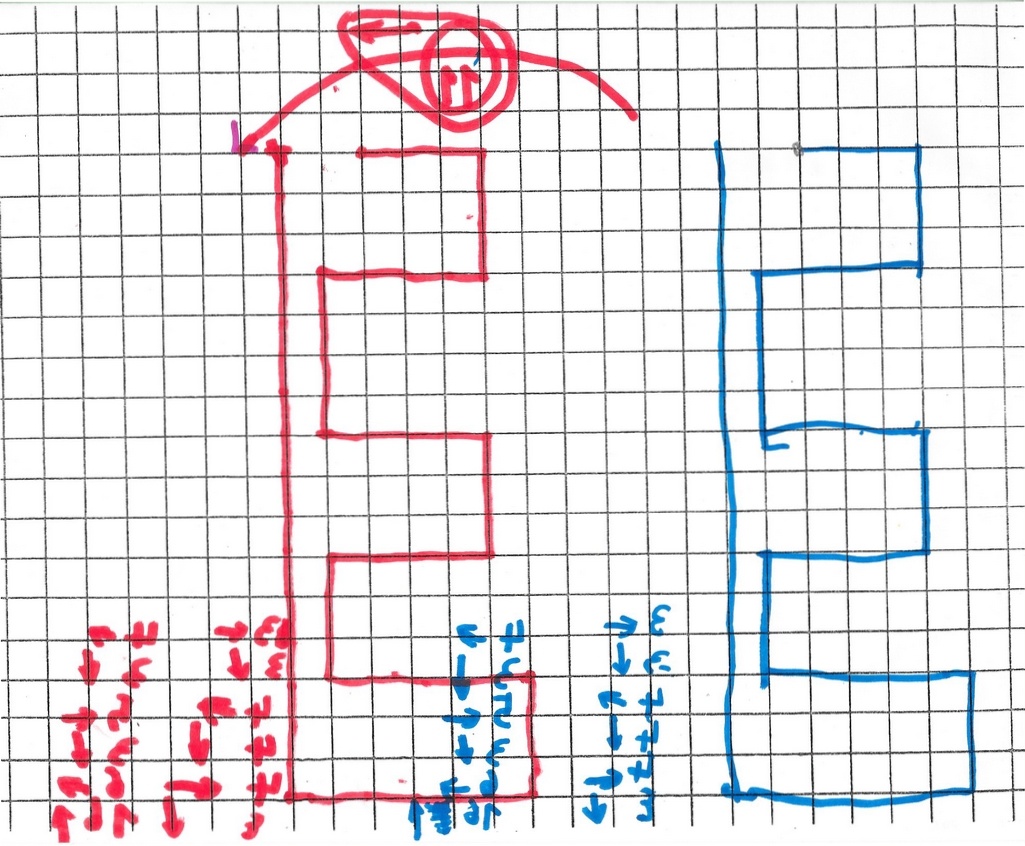
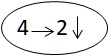 Michaël dessine quelques flèches, puis ne trace que les points d et a. La flèche n’est pas dessinée mais elle est « vue » quand même.
Michaël dessine quelques flèches, puis ne trace que les points d et a. La flèche n’est pas dessinée mais elle est « vue » quand même.