L’hypothèse d’Arthur
classes de cycle II et III : CP- CE1-CE2 | 6/9 ans | école 3 classes + 2 maternelles
recherche collective et individuelle
connexions : fonctions numériques, fonctions multiplicatives
Le contenu de la page
- vérifier la conjecture
- la vérité en mathématique
- remarques
Vérifier la conjecture
« La conclusion d’Arthur lors de sa présentation à la classe, et après avoir montré sa technique à l’aide de plusieurs exemples, il conclut : « le nombre de paquets et la moitié, c’est toujours le même nombre « .
Évidemment, certains essaient de le prendre en défaut :
» Et 5000, tu as essayé ? «
Arthur teste en direct et prouve que c’est vrai.
J’interviens :
» Et 8 532 ? 7 028 ? 100 000 ? «
Arthur, définitif : » Je ne les ai pas faits, mais si je les fais, je suis sûr que ça marche. «
La vérité en mathématique
Moi : « Peut-on dire que ton hypothèse est TOUJOURS vraie ?
A : On ne peut pas faire tous les nombres, il y en a trop !
M : Donc, tant qu’on n’a pas montré que c’est vrai pour tous les nombres, on ne peut pas affirmer que l’hypothèse d’Arthur est vraie. Il y a peut-être, dans la liste, quelque part, un nombre qui se cache et qui ne fonctionne pas. il faut dire que l’on ADMET l’hypothèse d’Arthur. Mais en mathématique, il faudrait apporter la preuve que c’est vrai pour n’importe quel nombre. »
Grand silence et grand vertige devant l’ampleur d’une tâche impossible.
Par contre, si jamais l’un d’entre vous trouve un nombre qui « n’obéit pas » à l’hypothèse d’Arthur, alors là, il faudra qu’on dise qu’Arthur s’est trompé.
Cette situation aborde le problème des quantificateurs en mathématique :
Pour que l’hypothèse d’Arthur soit vraie, il faut qu’elle le soit dans tous les cas, c’est à dire quel que soit le nombre n (∀ n) choisi dans l’ensemble étudié (ici N l’ensemble des nombres naturels)
∀ n ∈ N
On dit que « ∀ » est le quantificateur universel.
Par contre, si un seul exemple contredit l’hypothèse (∃ n), alors celle-ci est considérée comme fausse.
On dit que « ∃ » est le quantificateur existentiel.
Je termine, énigmatique :
» Des mathématiciens ont prouvé que c’était vrai toujours ! Ils ont apporté la preuve en faisant une démonstration. »
La technique opératoire adoptée par Arthur suppose la maîtrise de certains concepts :
– la notion de décomposition numérique : 114 —> (40,40,20,10 et 4)
– la notion d’exploration « verticale »* : par exemple, l’addition de deux nombres dans le monde des perles (40+40) se conserve pour leur image dans le monde des paquets (20+20).
Ces notions, comme bien d’autres, les enfants les côtoient dès le plus jeune âge, dans le domaine du non-numérique :
– notion de décomposition :

C’est une loi de décomposition de prénoms. Son signe est – . D’ailleurs, Jean-Charles, comme Marie-Paule ou Anne-Marie sont appelés prénoms composés. Grand-mère, rouge-gorge, croque-monsieur sont aussi des mots composés.
Samuel a inventé un objet composé qu’il a décomposé : il a appelé la loi, loi S.
– notions d’exploration « verticale »,
Certaines actions (additionner ici) dans le domaine de départ (nombre de perles) sont conservées dans le domaine d’arrivée (nombre de paquets). Ces notions peuvent être abordées avec de très jeunes enfants (5 ans et moins) dans le domaine non-numérique comme par exemple dans des situations de jeu corporel, de mimes : deux enfants : une fille, un garçon ; la fille lève le bras gauche, le garçon l’imite. La fille s’accroupit, le garçon … fait pareil. Ce qui se passe pour la fille est conservé chez le garçon.
On peut évidemment varier les actions, et même, au lieu d’obéir toujours, cette fois, désobéir : la fille s’accroupit, le garçon lève le bras.
La conservation des actions n’est plus respectée. Le garçon peut soit faire n’importe quoi, et dans ce cas, ses actions seront imprévisibles, soit désobéir de façon plus « calculée » ; à chaque fois que la fille s’accroupit, le garçon lève le bras gauche. Et donc à chaque action de la fille correspond une action du garçon. Les concepts de détermination et de fonction sont approchés. Le champ d’exploration est immense…
Il existe également une exploration « horizontale » : l’image d’arrivée est « calculée » directement à partir de l’objet de départ (ici une invariance de position de la zone hachurée)
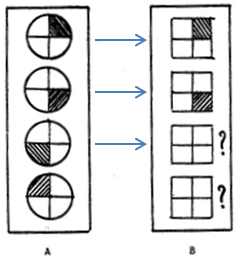
plus de précisions dans domaines math/présentation/explorations
Une autre démarche générale
Dans les recherches précédentes (le drôle de papa par exemple), on essaie de reproduire le phénomène (dessiner des objets symétriques) puis de l’explorer, voir ce qui se passe pour découvrir un savoir-faire, accéder à la maîtrise d’une technique opératoire efficace.
Avec l’hypothèse d’Arthur, la situation est différente : une technique opératoire est proposée d’emblée : « Pour trouver le nombre de paquets, je cherche la moitié du nombre pair ». Il s’agit alors d’en vérifier la validité.
Nous sommes en présence de deux démarches différentes.
voir des recherches/ démarche générale : routines et domaines math/présentation/routines
