routines
préambuleLe contenu de la page
- les routines : définitions
- des routines pour l’enseignant
- des routines pour apprendre à voir
- des routines pour agir
- les routines : historique
- analyse des productions
- une synthèse théorique
- une tendance statistique forte
- l’élaboration des routines
- analyse des productions
- les différentes routines
- des routines spécifiques
- des routines générales
- Les routines des enfants
- une routine, ce n’est pas
routine : définitions
XVIe siècle. Dérivé de route, au sens de « chemin très fréquenté ».
Selon le CNRTL (Centre National de Ressources Textuelles et Lexicales) :
1. Vieilli :
Connaissance, habileté acquise par l’expérience, la pratique plus que par l’enseignement ou l’étude.
2. Péjoratif :
– Habitude de penser ou d’agir selon des schémas invariables, en repoussant à priori toute idée de nouveauté et de progrès.
– Acte régulier et machinal, fruit d’une habitude plus que d’une réflexion.
– [Précédé de l’art. déf.] Opinion préconçue et immuable qui entrave le changement, le progrès.
3. Informatique :
Tout ou partie d’un programme ayant un emploi général ou répété.
notre définition
Ce sont nos quelques renversantes visites dans la classe unique de François Pâques à Bermicourt qui ont initié notre réflexion sur le concept de routine en recherche libre math.
Lors des recherches en math, celles sur les fonctions numériques par exemple, les enfants se posaient de façon récurrente certaines questions précises auxquelles il était important de répondre pour aborder et découvrir le phénomène étudié *.(comment ça marche ? A quoi ça ressemble ?…). C’est cette « feuille de route » qui alimentait le processus de recherche.
Nous avons constaté également, lors de la production de livrets de géométrie pendant nos stages internes d’autoformation que des constantes apparaissaient et suggéraient aussi des « étapes » dans leur développement (essayer de reproduire le phénomène étudié, collecter des données, les explorer,…)**
Certaines de ces tendances apparaissaient égélement dans les recherches libres de classe.
C’est la compilation, l’analyse et la synthétisation de cet ensemble d’invariants que nous avons appelée des routines.
La routine est donc une synthèse théorique conçue à partir des démarches individuelles et collectives de résolution réussies (partielles ou plus abouties) et réutilisées. On en trouve les traces dans les patrimoines de proximité.
Donc à la fois « un chemin très fréquenté », et « une connaissance acquise par l’expérience », mais aussi « l’emploi général ou répété » de l’informatique.
Mais dans tous les cas, elle est issue d’un savoir construit personnellement ou intégré à partir du savoir partagé des pairs ou de celui de l’adulte.
* voir «Nouveaux développements de la pédagogie Freinet», ouvrage cité précédemment.
** voir dans cette partie 3 le chapitre « invariants«
des routines pour l’enseignant
Ce qui empêche en partie la recherche libre dans la classe, c’est l’enseignant et sa peur : « Je suis nul-le en math. », « Je ne vois pas les situations intéressantes. », « Je ne sais pas comment faire. », « Je ne sais pas comment aider les enfants. »,…
Des routines pour apprendre à voir
Les routines sont des éléments utiles à l’élaboration de la culture nécessaire à la pratique de la recherche libre mathématique.
*voir globalement pour agir localement.
Des routines pour agir
Comment gérer la part de l’adulte dans le processus de recherche de l’enfant ?
Comment agir à bon escient, quand intervenir, quand donner le coup de pouce ou laisser faire ?
Moins l’enseignant est stressé, plus il sera confiant et ouvert, et laissera progressivement l’enfant exprimer ses propres représentations et construire sa mathématique.
Les routines participent à l’élaboration du minimum de culture mathématique intégrée nécessaire à l’apparition de la confiance en soi de l’adulte.
Si on ne sait pas comment démarrer, on peut dans un premier temps changer la structure de la leçon de math habituelle en s’inspirant des différentes étapes du déroulement de la routine générale : reproduire ou représenter la solution problématique de départ proposée, collecter les données, etc.*
De toute façon, les représentations personnelles des enfants auront, même dans le cadre d’une recherche fortement encadrée qui ménage néanmoins quelques moments de recherche libre, bien plus l’occasion d’émerger et de se manifester qu’au cours d’une leçon classique.
Si on ne veut pas se sentir dépassé ou démuni, on peut s’essayer à la recherche collective sur un sujet unique et avancer prudemment et progressivement avant de diversifier les sujets d’étude en cours répartis dans plusieurs groupes.
Les exemples proposés dans la présentation des routines** peuvent servir de déclencheur pour l’adulte.
On peut se référer à la routine pour débloquer une situation de recherche qui semble dans l’impasse.
Le fil rouge qui peut guider l’adulte serait la conscience d’abstraire pendant le processus de résolution : comment la réalité est-elle représentée, quelles caractéristiques a-t-on laissées de côté ? (une photo, un dessin ou une croix représentant un enfant ne sont bien sûr, pas équivalents).
* voir la partie 3 comment ?
** voir toute la partie 4 domaines math
petit historique des routines
analyse des productions
Une synthèse théorique
L’analyse, par les quelques enseignants impliqués dans le projet à l’origine, des recherches libres d’enfants, complètes ou partielles, d’essais déstructurés ou encourageants, de petits cheminements testés, abandonnés ou au contraire poursuivis, des défis posés, des questionnements, des directions suivies, des solutions apportées à chaque nouveau niveau d’abstraction atteint, des motivations des chercheurs, a abouti à la compilation d’un certain nombre de stratégies de résolution, de processus de construction de concepts qui ont réussi.
Les démarches qui ont abouti ont été synthétisées à partir de multiples éléments puisés dans les recherches et dans le patrimoine de la classe puis ont été écrites. On les appelle routines.
Les routines apparaissent comme un recueil d’actes réussis, un réservoir (non limitatif) de possibles qui peuvent s’actualiser ou pas dans la démarche du jeune chercheur.
Elles ont pour ambition d’aider l’enseignant dans l’acquisition de la culture mathématique nécessaire et de la maitrise technique de la recherche libre mathématique : accueillir en classe les événements prometteurs, accompagner sereinement l’enfant dans sa démarche tâtonnante de recherche et de construction de concepts mathématiques, couvrir les programmes officiels de l’école, du collège et plus.
Une routine apparaît ainsi comme un concept théorique résultat d’une analyse de recherches libres mathématiques d’enfants, individuelles ou collectives et de leur synthétisation.
Une tendance statistique forte
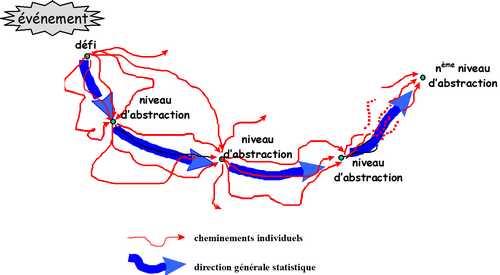
Les routines témoignent de l’histoire des cheminements choisis dans un processus de recherche ouvert et non balisé : pas de parcours programmé, pas d’étapes prévues à priori, mais un itinéraire à construire, à créer avec, comme fil d’Ariane, un projet de recherche issu de la problématisation de l’événement clairement défini.
L’expérience personnelle et collective augmente avec la multiplication des recherches. Les chercheurs élaborent des procédures de plus en plus efficaces et rapides, procédures qui peuvent être réinvesties dans d’autres situations.
Il y a DES réponses possibles au défi initial. Chaque avancée dans la résolution du défi se concrétise par une représentation nouvelle de la situation, abstraite de l’étape précédente. A chaque niveau d’abstraction, plusieurs représentations sont possibles.
Les cheminements individuels sont innombrables et variés (hétérogénéité). Ils s’orientent cependant suivant une direction générale qui, elle, paraît globalement et statistiquement invariante (homogénéité).
Un changement de type de représentation correspond à une montée en abstraction. Il dépend des besoins et des choix du chercheur : la solution choisie lui convient-elle ? Est-elle valide, assez économique, suffisamment rapide ?
élaboration des routines
De la disparité des processus singuliers de résolution à la routine
Un événement qui suscite l’intérêt devient après problématisation un point de départ d’investigation : un objet de recherche est posé. Le défi : comment y répondre ? Le processus de résolution peut démarrer. Chaque cheminement est singulier. Chaque exploration est différente et les solutions apportées diverses.
Des situations apparemment différentes (par exemple le bateau, le jeu du cheval, se ranger, danser en couple, faire équipe à deux…) ne sont pas, dans un premier temps, traitées de la même façon.
Cette hétérogénéité fait cependant apparaître des invariances dans leur déroulement, dans les processus d’abstraction dont la compilation à postériori par les enseignants a abouti à la rédaction de routines.
Les différentes routines
Une vingtaine de routines spécifiques étroitement liée aux domaines mathématiques abordés décrit les différents champs d’action des jeunes chercheurs.
Trois routines générales (« méta-routines ») s’en dégagent et font émerger une certaine homogénéité dans les démarches.
Des routines spécifiques
les domaines maths
Ce sont les situations de vie rencontrées en classe et à l’origine des points de départ de recherches qui ont déterminé le choix des domaines mathématiques* : mathématique non-numérique, mathématique numérique, géométrie et structures.
Quelques concepts fondamentaux y ont également contribué :
. la logique : oui/non, et, ou, si…alors, les quantificateurs ∀, ∃ ;
. les ensembles, les propriétés ;
. les relations ;
. les fonctions ;
. les lois, les groupes.
Ces domaines sont suffisamment étendus pour couvrir les demandes des programmes officiels, et aller même au-delà.
* voir la partie 4
Des routines générales
Une analyse portant sur les routines elles-mêmes a dégagé une routine d’un niveau plus général (routine de routines ou méta-routine) qui se décline, selon les situations envisagées, en trois routines parallèles.
Les situations/événements sont classés suivant les concepts mathématiques sous-jacents * :
– les situations qui relèvent des notions de propriétés, de relations (non fonctionnelles) dans lesquelles il s’agit de collecter, conserver, organiser des données et trouver des outils performants de représentation et de résolution (graphes, tableaux, diagrammes, …) : leur traitement est synthétisé dans la routine générale 1 ;
– les situations fonctionnelles qui amènent à la construction de techniques opératoires (x 4, savoir faire une symétrie axiale, …) : leur traitement est synthétisé dans la routine générale 2
– les situations de conjectures : leur traitement est synthétisé dans la routine générale 2bis
* tous ces concepts sont approfondis dans la partie 4 domaines math
Les routines des enfants
Pour répondre aux défis qui l’interpellent, l’enfant élabore des procédures de résolution qui se veulent de plus en plus efficaces et rapides.
L’analyse de la démarche choisie et la réflexion sur celle-ci apparaissent comme une préoccupation récurrente et quasi inévitable du jeune chercheur au cours du processus de résolution du problème posé. Chaque réussite (démarche partielle ou plus élaborée, solution apportée, technique opératoire, outil utilisés,…) est soulignée, commentée lors des présentations de travaux à la classe. Des liens sont faits avec d’autres recherches, des ressemblances, des équivalences sont constatées. Si la solution proposée est définie clairement (description, conditions d’utilisation, mode d’emploi) et validée, alors elle rejoint le patrimoine mathématique de la classe.
Le patrimoine collectif de proximité, espace matériel et immatériel de rencontre des expériences personnelles de chacun et de l’intelligence collective de la classe, renferme ainsi un certain nombre de ressources (démarches, savoir-faire, procédures,…) qui sont utilisées selon les besoins (ou pas) et intégrées dans le patrimoine personnel de chacun.
Suivant leur niveau d’abstraction, ces « routines »
– qu’elles soient spécifiques : comment transformer comme la fée, continuer la frise du pull over, inventer une couronne pour la galette des rois, dire ce qui manque à 3 pour avoir 10, gérer les pas de Bertrand et du facteur, produire un symétrique avec un calque, …
– un peu plus étendues : reproduire une suite périodique de plusieurs motifs, construire la table x4 et savoir l’exploiter, être capable de produire une symétrie axiale sans machine,…
– ou qu’elles soient plus générales dans la gestion d’une situation : penser pour démarrer à reproduire la situation, récolter des données, savoir les exploiter, …
Une routine, ce n’est pas…
– un modèle programmé qu’il faut absolument rechercher dans les événements et appliquer, en passant par toutes les étapes décrites, sans en oublier aucune. Les événements sont toujours plus complexes et les cheminements individuels plus divers ;
– un chemin obligatoire et identique pour tous qui s’opposerait à une démarche tâtonnante expérimentale et libre ;
– un algorithme, c’est à dire une procédure «description précise et rigoureuse d’une suite portant sur des informations qui permettent d’obtenir, en un nombre fini d’étapes, la solution d’un problème.»
– un remède miracle: une bonne formation mathématique de l’adulte n’est pas superflue.
Une recherche math ne se réduit pas à une routine, et une routine ne décrit pas toute la recherche math : la carte n’est pas le territoire.*
Il n’y a pas d’antinomie entre les notions de routine et de liberté en recherche mathématique. Les routines ne s’inscrivent pas dans un objectif de programmation des apprentissages basée sur des procédures à suivre.
Elles constituent un réservoir de possibles qui s’actualiseront éventuellement dans les cheminements singuliers des enfants. Elles ont pour ambition de sécuriser l’enseignant et de l’aider dans la maîtrise de la technique exigeante de la recherche libre mathématique.
* voir les ouvrages portant sur la Sémantique Générale d’Alfred Korzybski.(wikipédia)