Le contenu de la page
4. suite de la recherche : exploration
5. découverte d’une technique opératoire
école : classe unique (section enfantine, cycle 2 et 3 : enfants de 5 à 11 ans
niveau concerné : cycle 2
recherche individuelle : Mickaël, entre 5 ans 1/2 et 8 ans.
domaines : géométrie de transformation, symétrie axiale
connexions : invariance, angle droit, distance, alignement, transformation ponctuelle, technique opératoire

Poursuite de la recherche
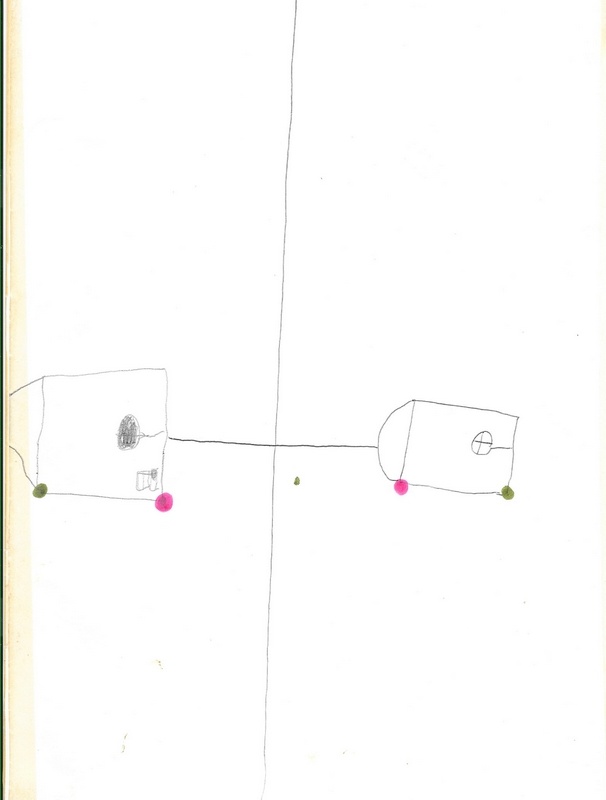
On reprend là où on l’a laissée : le problème de l’image des points.
Le redémarrage est difficile. (premier essai)
Je lui conseille donc de recommencer plus simplement.
D’abord il estime le point image, puis il vérifie en utilisant la machine pli-pointe.
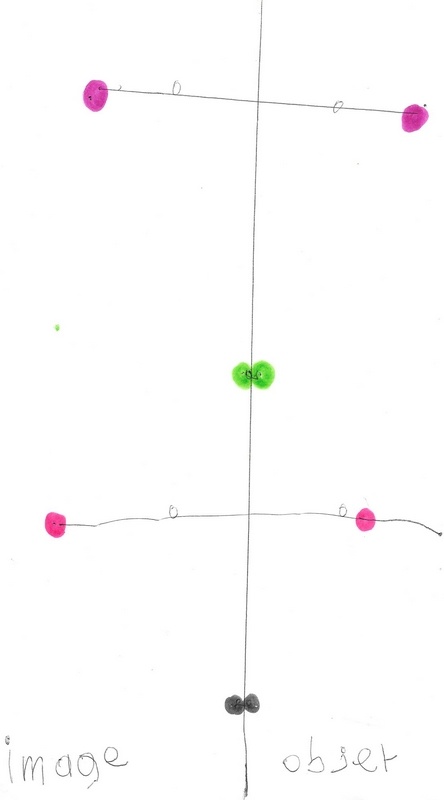
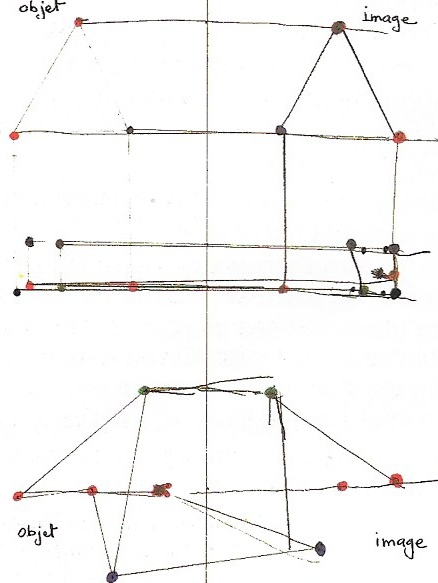
Estimation de l’image (point plein), vérification (petit point) avec le pli représenté ici par la ligne pointillée.
Mickaël cherche seul, puis une fois de temps en temps, demande à me voir pour montrer ce qu’il a trouvé. Il consulte aussi quelquefois d’autres enfants.
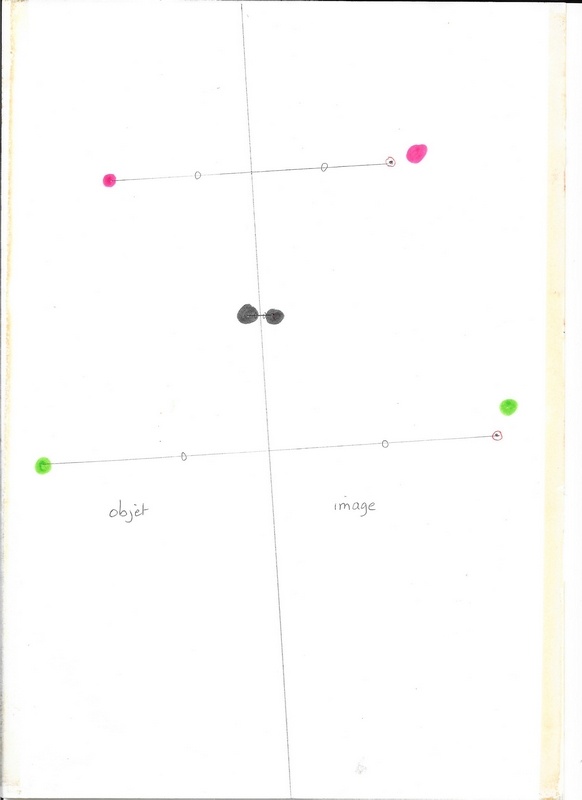
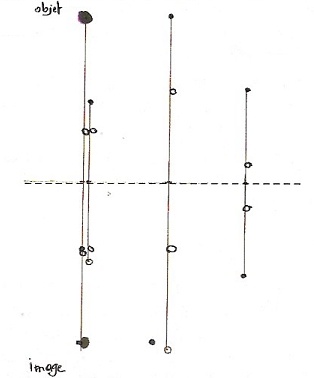
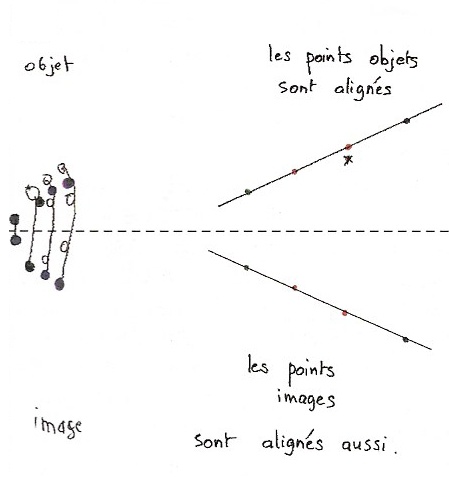
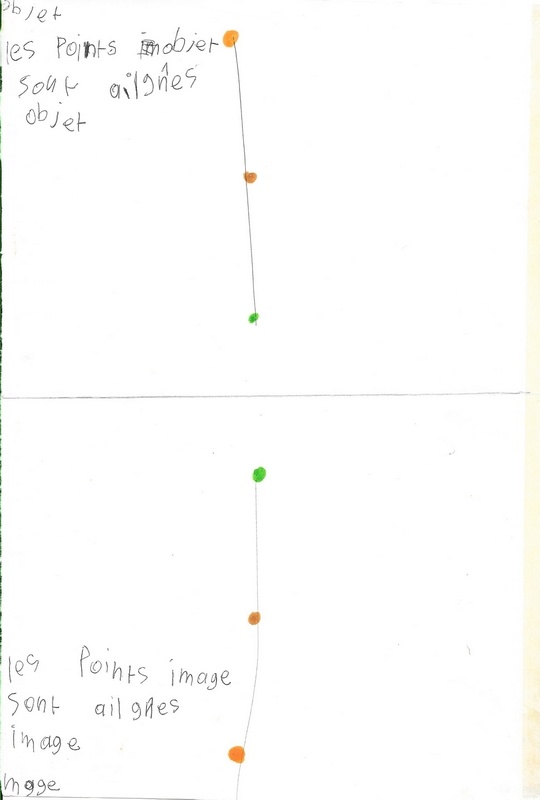
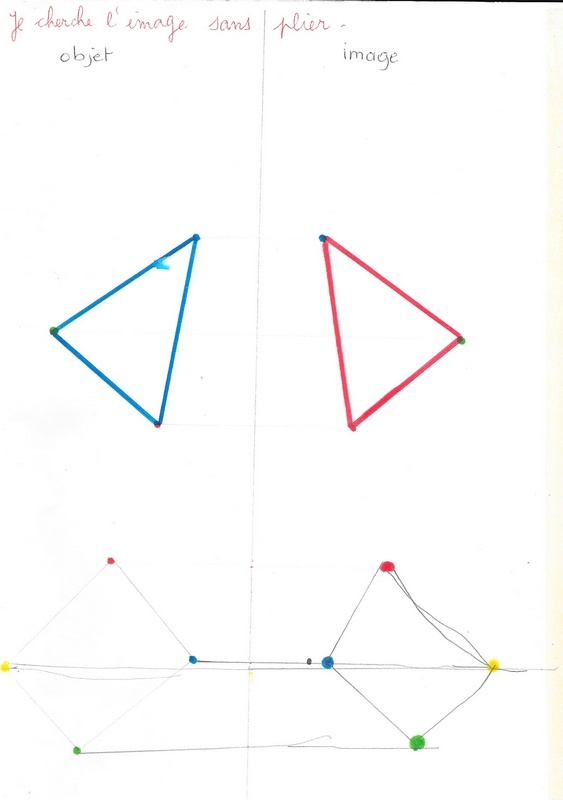
Une découverte fortuite (?) : les images de points alignés sont des points alignés :
à gauche : son travail ; puis à droite à partir de points objets alignés que je lui propose et la technique pli-pointe. On le fait ensemble.
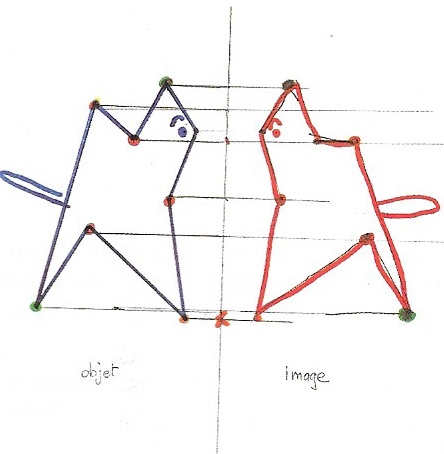
Dans l’essai de gauche, Mickaël cherche certainement dans un premier temps toutes les positions des images avec le pli et la pointe, puis il met les couleurs des points, mais il oublie « l’effet miroir » et se trompe.
A droite, avec moins de points, il n’y a pas d’erreurs.
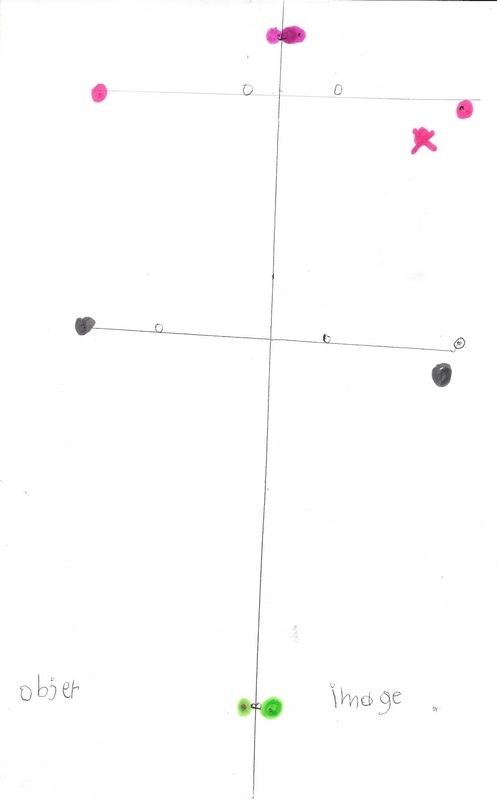
Utilisation des invariants
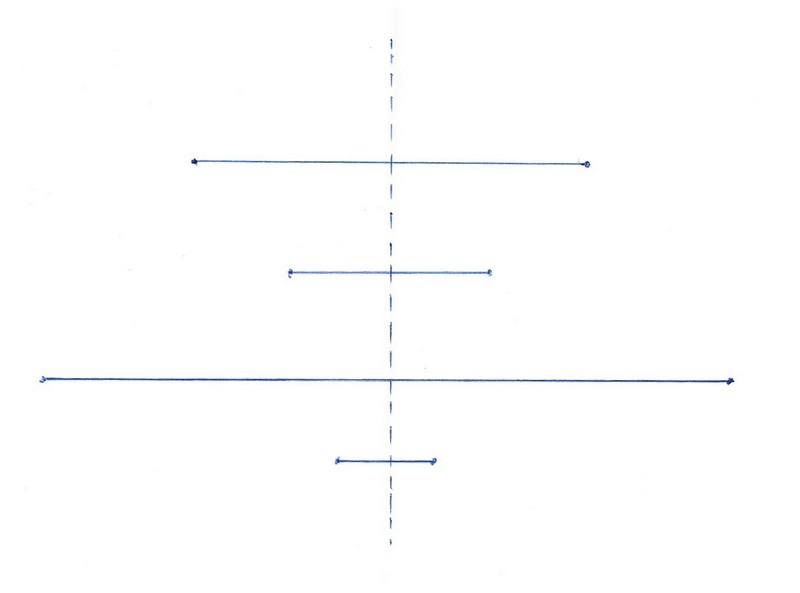
Utilisation de la bande de papier qui permet, en reportant fidèlement les longueurs, de respecter le premier invariant : l’égalité des distances par rapport à l’axe des points objet et image.
La figure du bas ne le satisfait pas : certains points ne sont pas « à la même hauteur ».
Pour régler le problème et après discussion avec lui, j’introduis le deuxième invariant qu’il a pressenti mais difficilement formulé : l’angle droit avec l’axe de symétrie. On utilise le coin de l’équerre. Il commence, à côté de moi, avec un dessin objet que je lui propose. Puis il travaille seul en utilisant le papier pour le report des longueurs, et le coin de l’équerre pour la perpendicularité à l’axe.
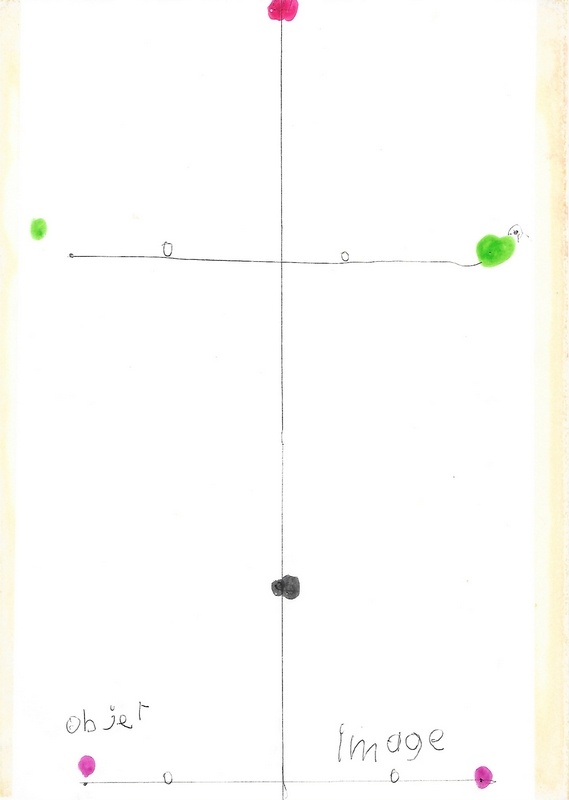
De nombreux essais avec la nouvelle procédure issue de la mise en lumière des deux invariants :
– papier pour les distances
– équerre pour la perpendicularité.
Pour reproduire une image symétrique, Mickaël se libère des « machines » utilisées précédemment. L’objectif permanent de l’image symétrique fidèle l’a obligé à une analyse de ses productions. Cette exploration lui a permis la découverte de ce savoir-faire « sans machine »
Au hasard (?) des tâtonnements :
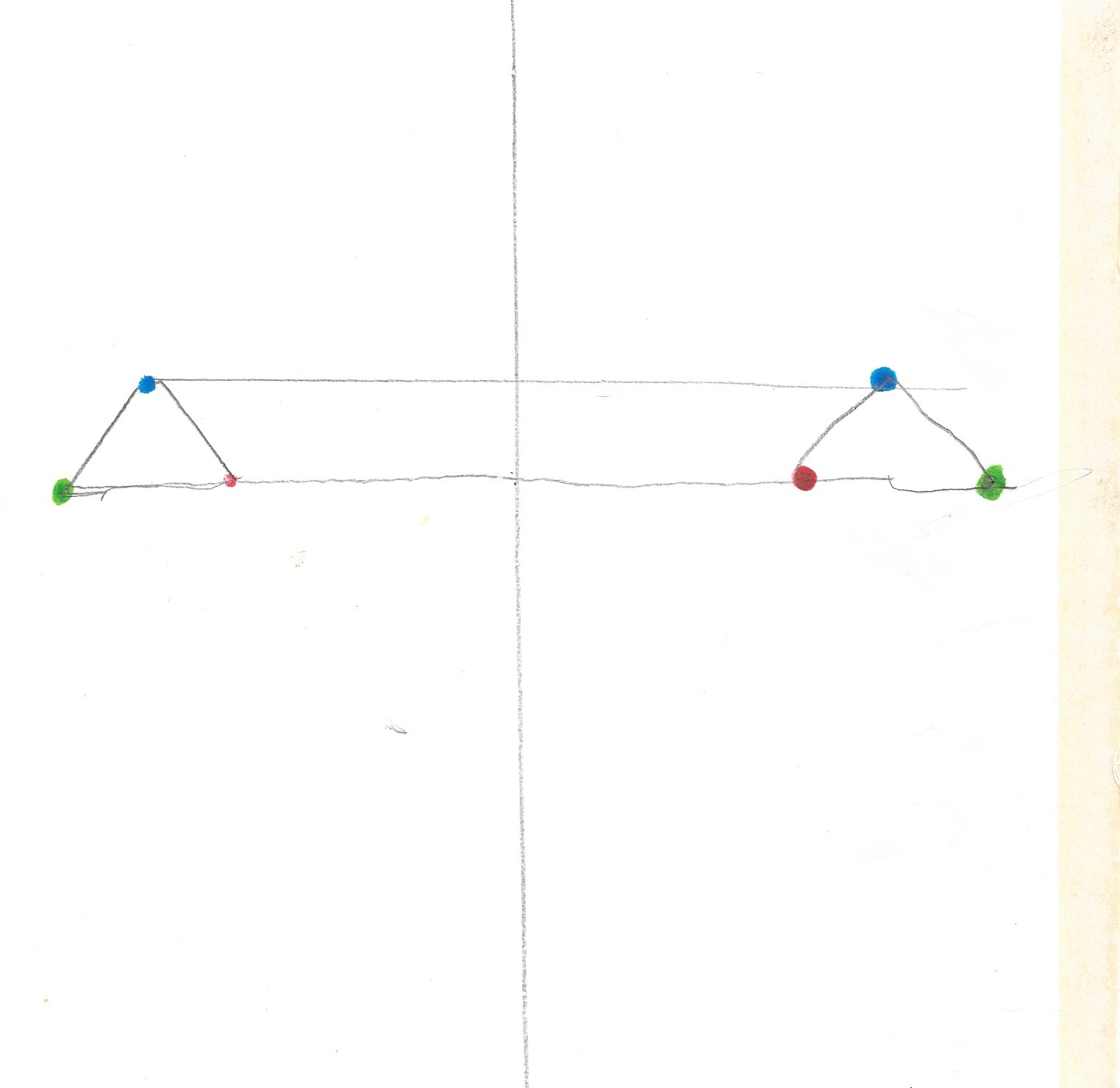
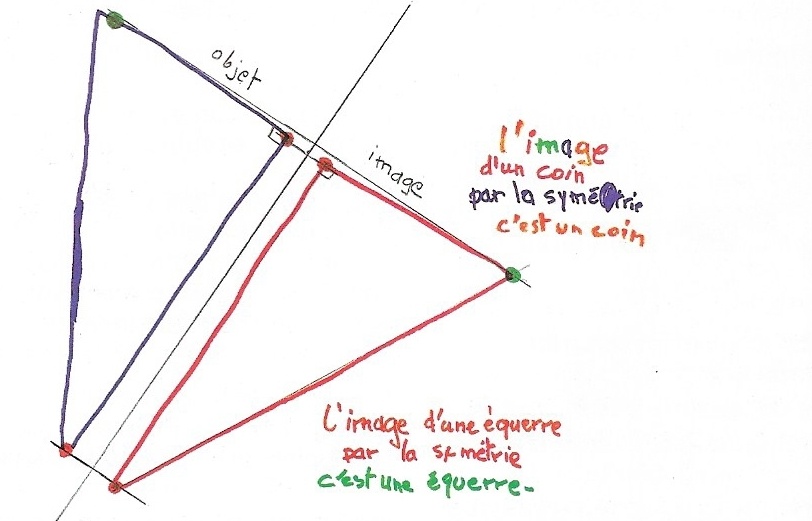
le symétrique d’un coin est un coin.
Le symétrique d’une équerre est une équerre.
Là, intervention de Bertrand (même âge) qui lui, travaille sur les translations :
Bertrand : « L’image n’est pas pareille.
Moi : – ? ;
B. : – Si je prends l’image et si je la mets là (sur l’objet), ça ne va pas. Le coin ne va pas.
Moi : – Quel déplacement fais-tu ?
B. : – Comme sur la tapisserie (translations)
Moi : – Mais là, chez Mickaël, est-ce la même transformation ?
B. : – ???
Moi : – Comment fais-tu Michaël ?
Mickaël : – Je plie. C’est pour ça que le coin est comme ça. »
Encore et toujours, il faut se frotter à l’autre, à ses représentations, à ses connaissances, à ses sollicitations…
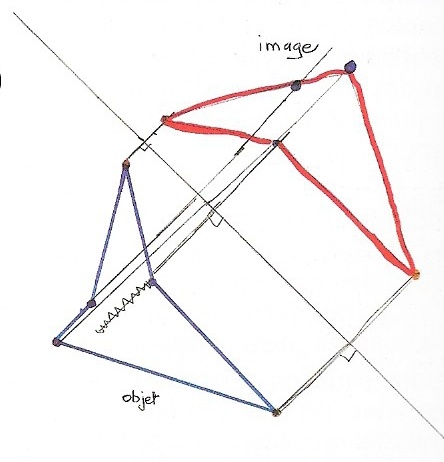
Les plus grands ont l’habitude (patrimoine mathématique de la classe), à la suite de l’étude d’une fonction, de la faire fonctionner plusieurs fois, à l’aide de la loi d’association * et de voir ce que ça donne.
Exemple : translation * translation * translation
Michaël me dit : « J’ai fini. Je sais bien faire les symétries maintenant. » Il présente son travail à la classe. Je profite de l’occasion pour relancer :
« Tu sais, Michaël, les grands, quand… »
C’est reparti. Il va composer deux symétries axiales.
A ce stade de la recherche, Mickaël utilise une technique opératoire de la symétrie axiale élaborée à partir des invariants qu’il a découverts. Ce savoir-faire le libère de la « machine », de l’outil matériel.
Avec plus d’entraînement, il pourra produire avec dextérité l’image symétrique d’un objet de façon très satisfaisante.
A force de longs et nombreux tâtonnements accumulés, ce « squelette » de la symétrie axiale qui représente (et symbolise aussi) l’invariance de la perpendicularité et des distances devient familier et s’inscrit profondément dans l’individu ainsi que dans le patrimoine mathématique de la classe.
Les nouveaux acquis sont encore fragiles et ont besoin d’être renforcés. Mais on peut dire que, à ce niveau, l’objectif de la recherche (produire une image symétrique) est atteint.
Des pistes évoquées :
– chercher des exemples de symétrie dans la vie de tous les jours, dans les magazines et faire un classeur avec les images et photos ;
– voir quel est le « squelette ».
Plusieurs questions qui se posent :
– Et si je change la règle des distances (distance objet = distance image), qu’est-ce qui se passe ? J’aurai un autre « squelette » et une autre transformation.
– Et si je change la règle du coin droit, que je prends un autre coin de l’équerre ?
– Et si je change les deux règles en même temps ?
Quand un sujet est exploré, le besoin d’aller voir plus loin surgit : et si ceci, et si cela… L’intérêt ne porte plus sur une situation de vie réelle particulière mais sur des êtres mathématiques, des représentations, des structures. La motivation du chercheur est intrinsèque*. Elle est l’énergie qui pousse l’individu à réaliser une activité pour le plaisir et la satisfaction qu’elle procure en elle-même, indépendamment de contraintes extérieures.
* voir « motivation autodéterminée » dans la partie 1 « la recherche ? » chapitre 4 « apprendre » et dans les annexes (Alain Guerrien* et Annie Mansy-Dannay)