le bateau 1
abstraire, représenterLe bateau
classe de cycle II : CP-CE1 | 6/8 ans | école 3 classes + 2 maternelles
recherche collective
connexions : fonctions, fonctions modulos
Le contenu de la page
- titre
- point de départ de la recherche
- la recherche
l’événement

Un enfant de six ans est allé dans un parc d’attraction et raconte le plaisir qu’il a eu de monter dans un petit bateau.
Point de départ
C’est la présentation du texte libre* et la discussion qui a eu lieu après.
A la suite de la lecture de chaque texte présenté, le président* de semaine (enfant choisi lors de la réunion de coopérative* hebdomadaire dont l’une des missions est de distribuer la parole) demande à la classe s’il y a des questions.
La question qui a le plus retenu l’attention :
« À combien on peut aller sur ton bateau ?
– À deux
– Moi j’aimerais bien pouvoir monter dedans !
– Moi aussi ! »
Il faut préciser qu’un bateau ne partait que s’il était complet : à deux par bateau. Tout le monde aimerait monter. On pourrait partir tous ensemble !
Question de l’enseignant :
– Si on avait assez de bateaux, est-ce que tout le monde pourrait partir (en même temps) ?
A priori, un grand nombre semble être sûr que oui. C’est le beaucoup qui a été entendu au détriment du deux par bateau.
La discussion à la suite du texte se prolonge : il y a un intérêt pour cette histoire. Tout le monde s’y voit dans ce bateau !
L’enseignant intervient aussi dans la discussion.
La question, tout en restant dans le sujet, n’est pas anodine.
Il y a une incertitude, une question à laquelle on n’a pas de réponse dans l’immédiat.
Comment faire ? Le défi est lancé. L’objet de la recherche est posé.
la recherche
On va essayer de jouer la réalité : les vrais enfants sont là, mais pas les vrais bateaux. Et on n’est pas près de l’eau.
Pour le bateau, on va prendre un cerceau, et on se place à deux par cerceau. Résultat : un enfant reste tout seul sur le bord (nous sommes 15) …
Mais on peut aussi se donner la main par deux, ou se tenir près l’un de l’autre…
Première tentative de re-présentation du problème. Les enfants jouent leur propre rôle, et les bateaux sont représentés par des cerceaux.
La propriété « être dans un bateau » se traduit par une autre propriété « être à l’intérieur d’un cerceau »
Cette première représentation du réel cache déjà une sérieuse abstraction de la situation initiale.
Abstraire, c’est choisir certaines caractéristiques d’un événement et en laisser de (très) nombreuses de côté.
Soit la situation 1 : ![]() et la situation 2 :
et la situation 2 : ![]()
On peut dire que la situation 2 est une abstraction de la situation 1 : une caractéristique n’a pas été conservée.
La situation représentée en classe ne tient pas compte de la forme, de la taille, de la couleur … du bateau. On a « oublié » le paysage, l’eau, la couleur du ciel, le soleil, tous ces éléments, importants pour pouvoir bien visualiser dans sa tête la situation, et qui étaient présents dans le dessin accompagnant le texte libre ou évoqués au moment des questions après la lecture. De nombreuses caractéristiques de l’événement ont déjà été abstraites parce que n’apparaissant plus comme essentielles. Si on avait voulu faire une représentation théâtrale, d’autres caractéristiques auraient été conservées (décors, bateau, …)
De plus, il a fallu représenter un élément (le bateau) et le remplacer ici par un cerceau (qui à priori a peu à voir avec un bateau mais qui conserve la propriété en jeu nécessaire : « être à l’intérieur »)
Quelqu’un dit : « Et avec les grands de la maternelle ? » Ceux-ci viennent chaque vendredi matin passer un moment pour travailler avec nous. A cet instant, ils ne sont pas présents dans la classe. Comment faire ?
Attendre vendredi, ou alors utiliser leur photo. On les a et on s’en sert souvent pour les maths. Il faudra mettre les photos dans les cerceaux.
Ou bien on dessine les bateaux sur une feuille, et on pose les photos dessus, puis on les colle, c’est plus pratique.
Le défi s’est un peu étoffé avec l’extension du domaine de travail : l’ensemble des enfants concernés a augmenté.
Une nouvelle présentation (représentation) de la situation est nécessaire.
Cette fois, les enfants sont représentés par des photos et les bateaux par des dessins.
De plus, « être dans le bateau » est représenté par « être collé sur le dessin du bateau ». C’est une propriété qui est en représentation.
Avec les grands de maternelle, tout le monde peur partir : il ne reste personne sur le bord.
C’est une deuxième abstraction de la situation.
Pas si pratique que ça…
Manipuler ces photos peut poser problème à certains en ce début de CP qui ont du mal à ne pas en égarer. Il faut donc vérifier que l’ensemble choisi (les photos) représente bien la réalité (les enfants).
Pour des enfants de cycle 1, les choses ne sont sans doute pas aussi simples. En effet :
Les couples représentation-représenté, c’est à dire photo-enfant, sont déterminés par une fonction f de Ph ensemble des photos, vers E, ensemble des enfants :
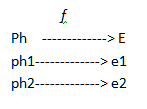
Très vite, des solutions sont trouvées pour les présents (CP) (correspondances terme à terme)
– distribuer les photos et vérifier : si je n’ai pas de photo, alors je le dis ;
– ou montrer la photo : l’enfant concerné lève la main : si je vois ma photo, alors je lève la main ;
– ou nommer la photo : l’enfant appelé se lève (si j’entends mon nom, alors je me lève) ;
Toutes les solutions ne se valent pas : la deuxième n’est pas très fonctionnelle si l’enfant ne laisse pas la main levée…
Revenons à la question qui nous préoccupe : « Tout le monde peut-il partir ? »
La place dans le bateau est-elle importante? Elle peut l’être. (être avec son copain, sa copine, ne pas être avec celui-là…).
L’est-elle pour le problème posé ? Non. Et la couleur du bateau ?
Et sa forme ? Et la position du bateau parmi les autres ? Et la distribution des enfants dans les bateaux ? Et le nombre de places dans le bateau ?
Quelles sont les données non-pertinentes pour le problème ? Et quelles sont celles qui le sont ? Tout ceci est à découvrir.
C’est le défi de départ qui constamment nous guide dans les choix des caractéristiques que l’on laisse ou que l’on garde.
Chaque nouvelle représentation adoptée révèle un changement de niveau d’abstraction.
Quand l’idée apparaît qu’il suffit de comptabiliser chaque enfant, hormis toute autre considération, alors, pour plus d’efficacité, le mode de représentation peut évoluer : comment représenter « l’essence » du problème ?
Il faut accéder à l’équivalence (par exemple) 1 enfant / 1 cube et 1 bateau / 1 boîte.
On peut alors abandonner photos et dessins pour une autre représentation: L’ensemble des enfants sera représenté par un ensemble de petits cubes. Il faut être capable de créer une collection équipotente (autant que). La pertinence du nombre cardinal pour la résolution du problème apparaît. Il sera très intéressant de vivre le fait que certaines actions sur les cubes (représentants) auront une traduction dans l’ensemble des enfants. L’idée générale des deux mondes reliés entre eux par un « passage» (la fonction), apparaît.
Le problème des bateaux est donc maintenant représenté par :
Si une croix est entourée, alors un enfant a sa place dans un bateau, «un» voulant dire n’importe lequel.
La seule idée pertinente qui reste pour la résolution du problème est ici le nombre, propriété d’ensemble. Les caractéristiques des éléments sont écartées.
On préfèrera par la suite à l’ensemble matériel de cubes un représentant plus pratique : un ensemble de croix (par exemple) muni d’une propriété p : « est entourée ».
Cette propriété p traduit une autre propriété q : « a sa place dans un bateau »
Le problème des bateaux est donc maintenant représenté par :
![]()
Si une croix est entourée, alors un enfant a sa place dans un bateau, « un » voulant dire n’importe lequel d’entre eux.
Et c’est bien là la difficulté. L’ensemble des enfants en tant que groupe d’individualités (« Et moi est-ce que je monte ? », « et mon copain ? ») doit être oublié. La seule idée pertinente pour la résolution du problème est ici le nombre cardinal, qui est une propriété d’ensemble et non une propriété d’élément.
Nouvelle représentation :
– une croix, c’est un élève
– une croix entourée veut dire qu’un élève a sa place dans un bateau
Mais elle est tout à fait intégrée parce qu’elle s’inscrit comme une nécessité, comme l’aboutissement naturel d’un cheminement construit pour la recherche de la solution au défi initial. » Tout le monde peut-il partir ? »
Cette dernière abstraction opérée pour accéder au choix de la représentation très épurée des croix entourées nous éloigne encore plus du réel pour le monde des signes.
Puis intervient la prise de décision : si toutes les croix sont entourées, alors on part. S’il en reste une non entourée, alors on ne part pas. Il faut savoir se plier aux contraintes du problème (c’est tout le monde ou personne, et deux par bateau obligatoirement) et ainsi renoncer à des propositions comme «celui qui reste, je veux bien le prendre dans mon bateau».
Le défi initial est donc relevé.
De plus, il faudra se rappeler pour une prochaine fois, de la démarche suivie pour trouver la solution.
De représentation en représentation, les abstractions successives construites ont amené à une technique opératoire de prise de décision efficace.
La conscience d’abstraire, à chaque étape, participe à l’élaboration d’un patrimoine personnel et collectif.
