L’hypothèse d’Arthur
classes de cycle II et III : CE1-CE2 | 7/9 ans | école 3 classes + 2 maternelles
recherche collective et individuelle
connexions : fonctions numériques, fonctions multiplicatives
Le contenu de la page
- événement
- l’hypothèse d’Arthur
- organisation de la recherche
- les groupements
- les nombres pairs
L’événement

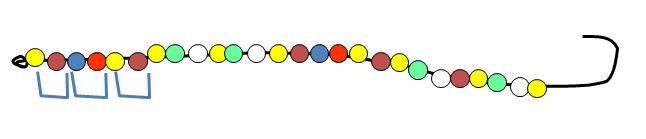
Comme chaque matin, le/la responsable présente les colliers du jour : le long et le court. (voir rituel 2) et les vérifie devant la classe en en comptant les perles : une par une puis 2 par 2 par la suite, et même trois par trois avec ceux qui savent.
Dans le groupement par deux, on constate rapidement que quelquefois, il reste une perle toute seule.
Et il/elle annonce pour cette journée du 26, qu’il y a 13 paquets de 2, et il reste 0 perle, ou 13 fois 2 paquets et il reste 0.
Vers 7 ans, la vérification par comptage des perles une par une devient longue et fastidieuse pour les colliers longs (> 20 perles). Il faut être plus efficace.
La technique des groupements par 2, par 3 apporte de la rapidité. Mais pour cela, il faut maîtriser les « listes de nombres » {2,4,6,8,…} {3,6,9,12,…}
A un moment ou à un autre se pose également la question du nombre de paquets formés (qui est donné par comptage dans un premier temps). Immanquablement, la remarque que le reste est toujours 0 ou 1 est faite.
Nous avons déjà constaté à plusieurs reprises que le comptage long pouvait être avantageusement remplacé par certains calculs. Dans de nombreuses situations, le calcul, c’est mieux que le comptage. Certes, mais encore faut-il savoir calculer…
L’idée que le calcul, quand il est possible, à notre portée, est une solution plus rapide et plus élégante s’installe tranquillement dans le patrimoine mathématique de la classe.
L’hypothèse d’Arthur

Le 26 novembre, après le comptage des paquets de 2, Arthur (8 ans) intervient :
« Pour trouver le nombre de paquets, je cherche la moitié du nombre pair ». Donc, nombre de paquets de deux et moitié, ce serait pareil.
Est-ce que c’est vrai ? Il faut vérifier ce que nous avons appelé « l’hypothèse d’Arthur ».
Habituellement, les points de départ des recherches naissent d’événements de la vie courante qui nous interpellent, nous étonnent, nous questionnent. La problématisation des situations qui s’en suit incite à des recherches qui passent par une collecte et conservation de données pertinentes, leur exploration et leur organisation, la découverte d’invariants et la construction d’une technique opératoire qui permettent de relever les défis soulevés.*
Mais cette fois, l’incitation vient d’une conjecture, celle d’Arthur, qu’il faut vérifier. Une proposition est donnée à priori et il s’agit de (dé)montrer sa validité. *
Dans le premier cas, une solution est à trouver ; dans le second, une hypothèse proposée est à vérifier.
* dans le menu voir l’onglet « des recherches/démarche générale : routines »
L’organisation de la recherche
Pour vérifier que l’hypothèse d’Arthur est vraie, il faut
– connaître les nombres pairs ;
– savoir trouver la moitié d’un nombre pair ;
– savoir faire et compter les paquets de 2 (avec le dessin ou autrement) même pour les grands nombres sans se tromper ;
– vérifier si la moitié d’un nombre pair, c’est pareil que le nombre de paquets de 2 ;
– dire si l’hypothèse d’Arthur est vraie.
Comme la conjecture intéresse beaucoup d’enfants, on décide de faire une recherche collective : tout le monde travaille sur le même sujet, mais chacun dans son coin tout seul, ou par petits groupes de 2-3.
Au bout d’un certain temps, une mise en commun par mini-présentations de ce que l’on a trouvé est faite à la classe, on discute et on repart vers sa recherche.
Ce va-et-vient régulier entre l’individuel et le collectif est le fondement même de la recherche collective.
Même si le point de départ est commun, les parcours personnels sont variés et les propositions de solutions plurielles. Chacun peut reprendre à son compte une technique présentée jugée intéressante ou poursuivre avec son idée première.
Il est même fréquent que de nouveaux centres d’intérêt émergent, sources de nouvelles recherches ultérieures.
Les groupements
De nombreuses situations de vie concrétisant les notions de groupements par deux et de modulo 2 sont abordées, étudiées dans le courant de l’année et viennent enrichir l’expérience individuelle et le patrimoine collectif de la classe.
Quelques points de départs :
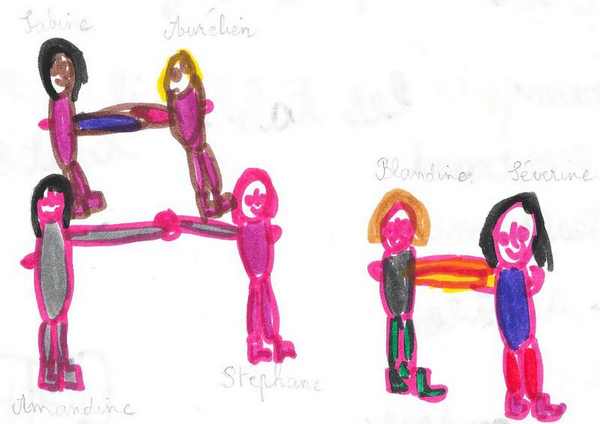
– Tous les jours, on se range par deux avant d’entrer en classe ;
– Le bateau du parc d’attraction (voir « des recherches ») ;
– En sport, beaucoup d’activités se font par équipes de deux ;
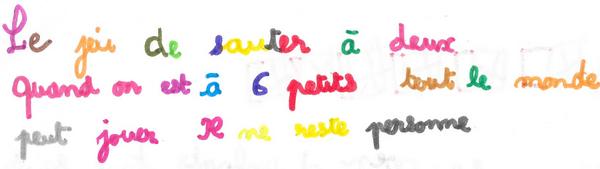
Ou un groupement par trois :
le jeu du dromadaire
Pour plus d’infos : voir dans domaines mathématiques, fonctions numériques modulos.

Les nombres pairs
La vie à l’intérieur et à l’extérieur de la classe (école, maison, correspondants, région, …) offre de nombreuses occasions de s’étonner, de s’interroger.
Les nombres pairs s’invitent dans de multiples situations à priori différentes mais qui à la longue, au fil des recherches et des découvertes, s’avéreront bizarrement posséder comme un air de famille…
Tous les matins, il faut vérifier les colliers de perles. Être capable de « deviner », avant de les grouper par deux, s’il va en rester 1 ou 0 suppose la maîtrise des nombres pairs/impairs.
Les compositions de fonctions :
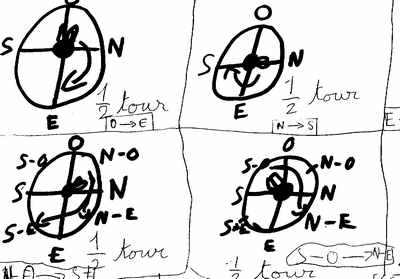
dans le numéro de la date (1996), le 9 et le 6 se ressemblent : à partir du 9, j’obtiens le 6 en le tournant (1/2 tour)
Si je tourne 4 fois, c’est comme si je n’avais rien fait. Tous les nombres pairs présentent le même résultat (reste 0 dans le modulo 2)
La direction du vent :
Dans le ciel, en altitude, les nuages vont vers l’ouest, et au sol, la girouette indique l’est.
O —> E
C’est un demi tour. Si je fais plusieurs fois le changement …

Le crocodile de Thomas
Thomas a montré à la présentation d’objets* un crocodile qui fait de la lumière quand on appuie sur la queue. Quand on lâche, ça s’éteint.
Le crocodile est fermé au départ. Je change 8 fois. Quel sera le résultat ?![]()
Comme si je n’avais rien fait.
Et si je change 19 fois ? 24 fois ?
A l’occasion de recherches sur de nombreux événements de vie comme les groupements par deux, certains changements réitérés (faire un demi-tour plusieurs fois, retourner un objet plusieurs fois, allumer/éteindre une lumière, …) mettent en lumière, dans chacune de ces situations apparemment différentes, et de façon totalement inattendue pour les enfants (5-8 ans), la même liste de nombres particulière {0,2,4,6,8………. 26,28,….}.
Les paquets
Voici en partie un début de recherche d’un enfant de CP (6/7 ans) sur le jeu du dromadaire. Le dessin figuratif initial des éléments (enfants) est remplacé par une représentation plus rapide : la croix.
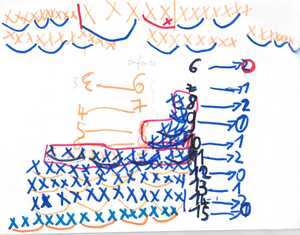



Cette activité de dénombrement amène le chercheur dans un premier temps à envisager des défis qui portent sur des situations » maîtrisables » (on reste prudemment dans le domaine du connu). Mais peu à peu, les défis que l’on se lancent deviennent plus ambitieux.
Dans tous les cas, le nombre d’essais que l’enfant se donne est toujours impressionnant, bien au-delà de ce qu’un enseignant oserait demander. Et cette profusion augmente significativement l’expérience et la familiarité numériques de chacun.
La recherche d’exemples se fait au début de façon « sauvage », au hasard. Mais très vite, des petits problèmes à régler surgissent, et parmi ceux-là, celui des doublons. Fréquemment, on retrouve plusieurs exemplaires identiques de la même situation. Les feuilles de résultats un peu « fouillis » ne sont pas toujours très lisibles. Et quelquefois, la poursuite de la production de nouveaux exemples pose problème. (« je l’ai déjà fait ? »)
Ceci est évoqué lors des présentations intermédiaires des travaux à la classe : les propositions du groupe sont recueillies, discutées (comment peut-on faire ?) et l’avis des plus expérimenté(e)s qui ont déjà été confronté(e)s à ce type d’obstacles est écouté (comment avez-vous fait ?).
Ainsi, devant des problèmes récurrents, se construit peu à peu un ensemble d’actes réussis que les enfants s’approprient et qui nourrissent le patrimoine mathématique de la classe. On apprend à apprendre coopérativement.
Et pour les recherches ultérieures, « chercher les exemples dans l’ordre » est une consigne qui est adoptée parce que fructueuse, motivée et intégrée par l’individu.
Une autre technique
Dans 29, combien de paquets de 2 ?
Avec l’utilisation des listes de nombres ( {2,4,6,8,…} un système « mixte », entre le comptage et le calcul est découvert :
– la bouche compte les perles : 2,4,6,8,10,12…
– en même temps, les doigts comptent les paquets : 1,2,3,4,5,6…
Tiffany : « 20 perles, c’est 10 paquets. Mais après je n’ai plus de doigts pour continuer. Donc je recommence à 0 avec les doigts en me rappelant que j’ai déjà 10 paquets. Il m’en reste 9 à compter : 2 perles c’est 1 paquet, 4/2, 6/3, 8/4 et c’est tout. Il en reste 1 tout seul.
Donc 29, c’est 20 (10 paquets) et 9 (4 paquets, reste 1) 29, c’est 10+4 paquets reste 1.
Pour 36 :
Je vais plus vite : 20, c’est 10 paquets puis je compte le reste jusqu’à 36. »
Kelian : « On peut aller plus vite encore : 20, c’est 10 paquets ; 10, c’est 5 paquets et les 6 qui restent, je les compte. » (doigts, bouche)
Pour aller vite, il faut calculer le plus possible, et compter le reste. On calcule pour les dizaines et on compte le reste.
Il faut conserver les résultats que l’on découvre pour ne pas les recherche à chaque fois, essayer d’en mémoriser quelques uns.
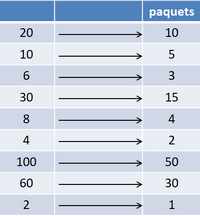
Ce tableau de résultats à conserver facilite grandement le calcul du nombre de paquets. Mais comme il s’étoffe rapidement, il devient de moins en moins maniable et efficace. Il faut le faire évoluer, le simplifier, trouver une liste la plus courte possible mais qui permet néanmoins le calcul pour tous les nombres, même les plus grands … C’est un nouveau défi à relever qui emmène le chercheur vers la construction de la liste ultime : la TABLE des moitiés.
Voir math numérique/fonctions numériques.