la marche des facteurs
problématiserLa marche des facteurs
section CE| 7/9 ans | classe unique 4/11 ans
recherche collective
connexions : fonctions, fonctions multiplicatives
Le contenu de la page
- titre
- point de départ de la recherche ;
- la recherche.
L’événement

Sandrine raconte aux nouvelles* : « Mon père a fait la marche des facteurs. C’est une course à St Pol. »
De nombreuses questions sont posées (Est-ce que ton père a gagné ? Quoi ? C’était quand ? … )
« Il faisait des grands pas pour gagner la course »
Une première re-présentation du réel : visuelle (photo) et orale.
Point de départ de la recherche
Dans l’étonnement général, elle a essayé de nous montrer les pas que faisait son père.
« Hou là là ! Nous on doit au moins en faire deux ou trois ! Et Bertrand (le plus jeune de la classe) quatre ! »
Une deuxième re-présentation du réel : jouée (comme au théâtre) qui révèle une nouvelle abstraction de la nouvelle de départ : on s’intéresse essentiellement aux pas du facteur. Et tout le reste est mis de côté (potentialisé).
A la suite des nouvelles (appelées aussi « quoi de neuf ? ») présentées chaque semaine, le président* de semaine (enfant choisi lors de la réunion de coopérative* hebdomadaire dont l’une des missions est de distribuer la parole) demande à la classe s’il y a des questions ou remarques.
« Ton père a dû faire beaucoup de grands pas ! Et si c’est Bertrand qui devait faire la marche !!! »
Malgré ses efforts, Sandrine n’est pas satisfaite des grands pas qu’elle fait : ils étaient plus grands que ça. Je me propose donc de faire le facteur. Un enfant marque par terre à la craie le début et la fin du grand pas du facteur. Bertrand fait ses quatre pas avec le même point de départ : on trace aussi les petits pas.
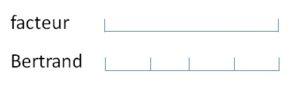
La nouvelle suscite l’intérêt, donc on prend un peu de temps pour trouver les réponses autour du nombre de pas que Bertrand devrait faire.
Nouvelles représentations/abstractions
On essaie avec deux pas de facteur :

Bertrand doit en faire 8 !
Les plus jeunes essaient de deviner : et 4 pas de facteur ? Les plus âgés se dépêchent de répondre. On vérifie : ils ne se trompent pas !
Et pour faire toute la longueur de la classe ?
Et la cour ? Et 100 pas de facteur ?
Les questions sans réponses sont nombreuses pour certains enfants de la classe. Les enfants du CM, eux, maîtrisent la situation et n’hésitent pas à montrer aux plus jeunes l’étendue de leur savoir et du pouvoir acquis.
La grande hétérogénéité des classes uniques d’alors était un atout considérable.
Nouvelles interrogations, représentations, abstractions. Nouveaux défis à relever.
Une recherche précédente
Cette recherche ressemble à une autre recherche, sur les trains, qui est présentée à la classe quelque temps avant : « grève en France, un train sur quatre part. »
Une discussion suit cette information délivrée par les deux responsables et les questions sont nombreuses : et si trois trains sont partis ? Et 7 ? Et 10 ?
Celui qui amène l’info (8 ans) est submergé. Les grands du CM prennent la relève : « Si c’est un train sur 4, ce sera deux trains sur 8, 3 sur 12. C’est comme la recherche 1 jeton, c’est 4 F, ou 1 an c’est 12 mois de David. Tu devrais faire la recherche parce que tu ne sais pas nous répondre. »
C’est décidé, il prend la recherche, avec un petit plan d’action : faire des dessins s’il ne trouve pas « directement », et des réponses à trouver : pour 3 trains, 7, 10 …
Deux enfants sont chargés de l’information : deux fois par semaine, ils relatent les événements importants qui se sont déroulés dans la région, en France et dans le monde. Si certaines informations méritent un complément, il faut aller chercher dans les journaux ou dans les livres (à l’époque – années 80 – le web n’était pas encore là).
L’évocation par les plus grands de recherches antérieures témoigne d’une expérience collective de classe accumulée au fil des présentations mathématiques à laquelle on peut se référer.
Au moment mathématique, il démarre donc :
1 train part sur 4 prévus
2 trains partent sur 8 prévus
et 3 ?
La liste va jusqu’à 20. C’est apparemment suffisant dans un premier temps pour commencer l’exploration.
Recours au dessin pour accumuler des données avec plus de sécurité : les trains sont représentés par des croix

3 trains partent sur 12 prévus.
Et 4 ?
 4 trains partent pour 12 prévus
4 trains partent pour 12 prévus
Cette recherche précédente sur les trains (comme toutes les autres recherches individuelles ou collectives) fait partie de la culture mathématique collective de la classe, vivante et incarnée par leurs auteurs : c’est la recherche de David, ou celle de Cédric … L’ensemble des savoirs construits dans tous les domaines alimentent le patrimoine culturel* de la classe.
Profitant de recherches antérieures sur les fonctions, il passe rapidement de

à

Assez rapidement apparaît le fait que quand j’ajoute 1 d’un côté, j’ajoute 4 de l’autre.
Il est acquis, vers 8 ans, que pour explorer ce type de situations, il est efficace de chercher beaucoup d’exemples puis de les ordonner.
Les croix et leur dénombrement sont abandonnés (trop long) au profit des nombres et du calcul.
Retour à la marche des facteurs
Cette exploration prise en charge par un enfant de 8 ans va se poursuivre. C’est la recherche de représentations nouvelles qui permet la résolution du problème.
Les différentes étapes dans la montée en abstraction sont évidemment franchies différemment selon les individus. Les cheminements individuels sont innombrables .
L’évolution de ce de type fonctions multiplicatives est développée dans la partie domaines mathématiques : ici
