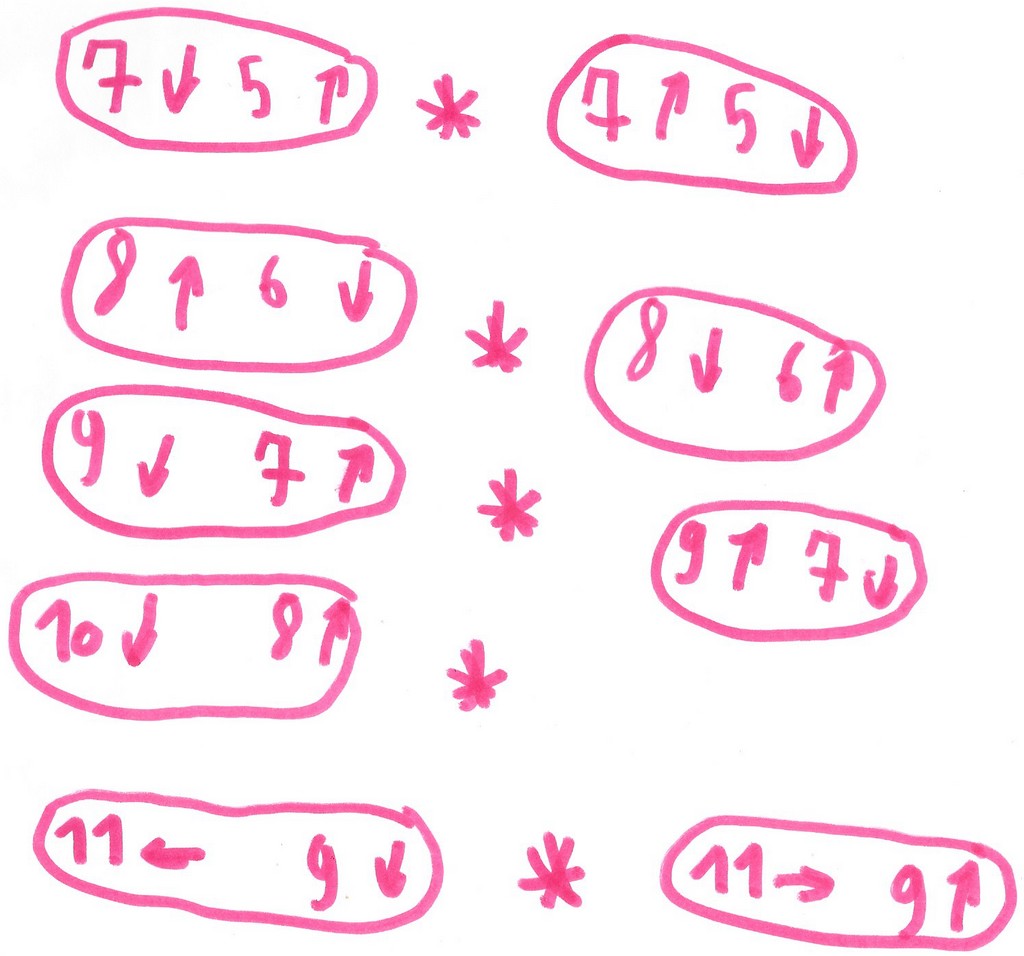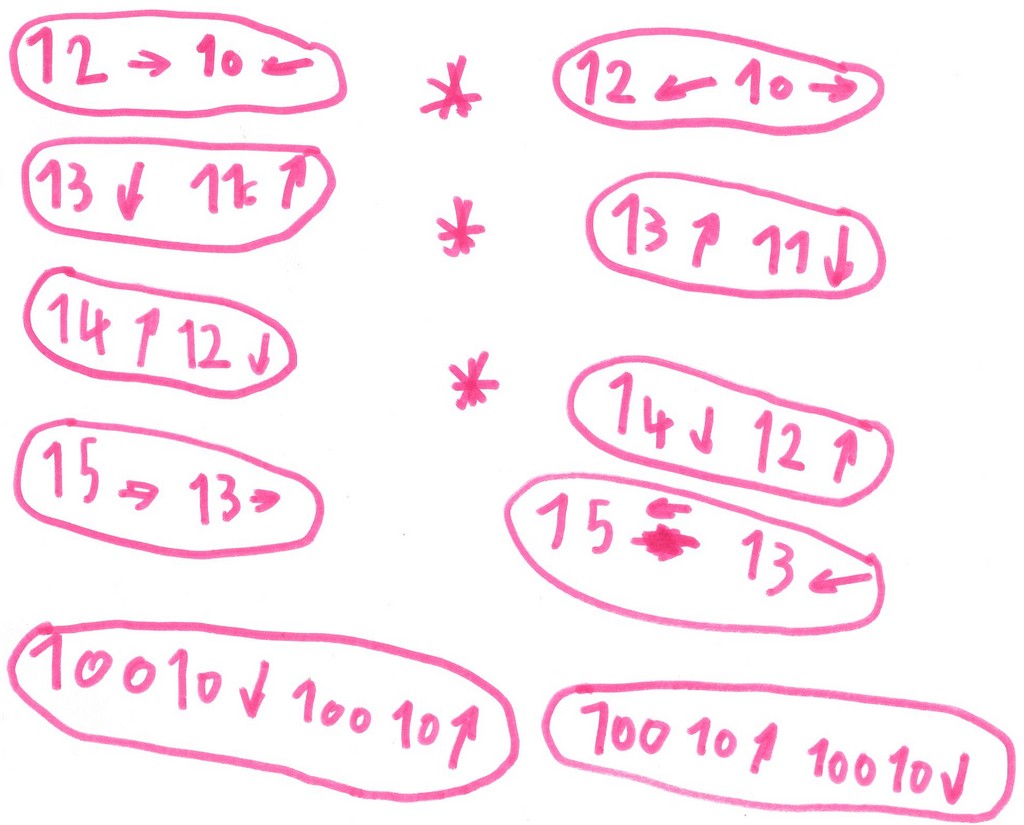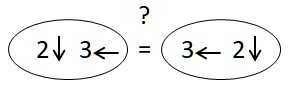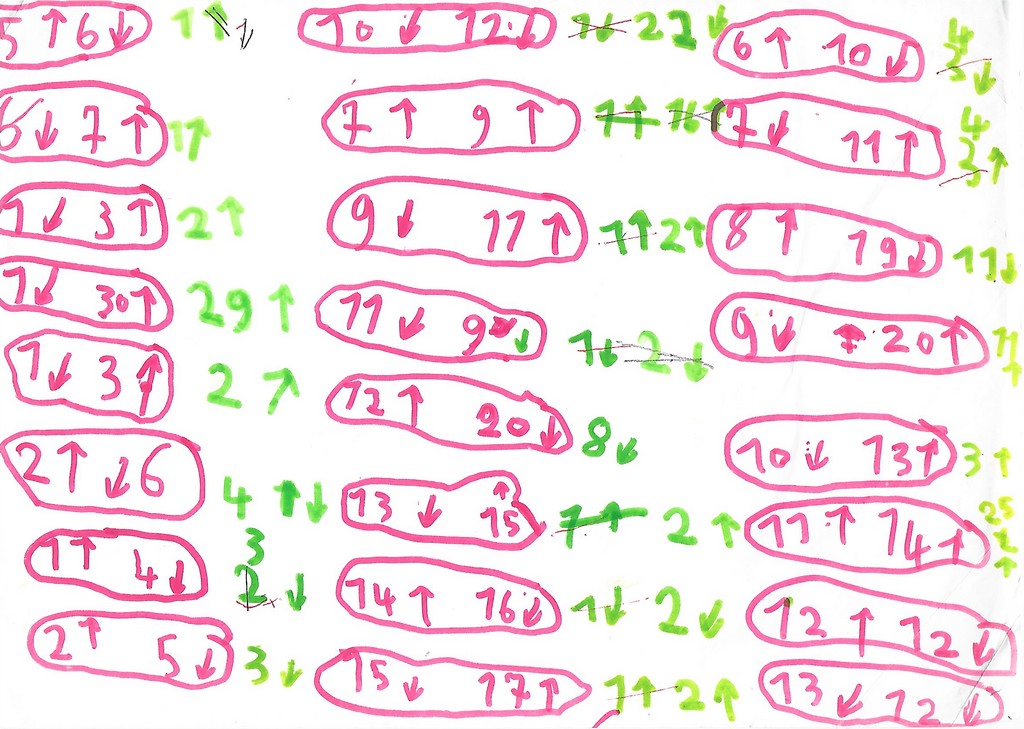Le contenu de la page
7. composition de translations, propriétés
école : classe unique (section enfantine, cycle 2 et 3 : enfants de 5 à 11 ans
niveau concerné : cycle 2
recherche individuelle : Mickaël, entre 5 ans 1/2 et 8 ans.
domaines : géométrie de transformation, translation, composition de translations, structures
connexions : vecteur, groupe
composition de translations, propriétés
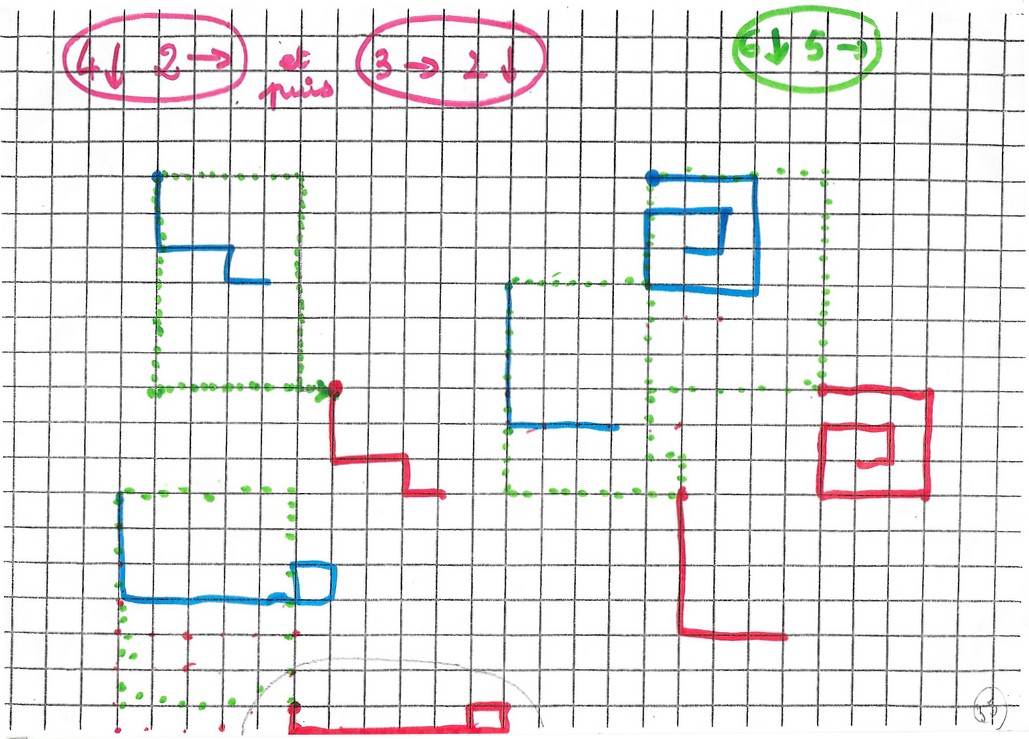
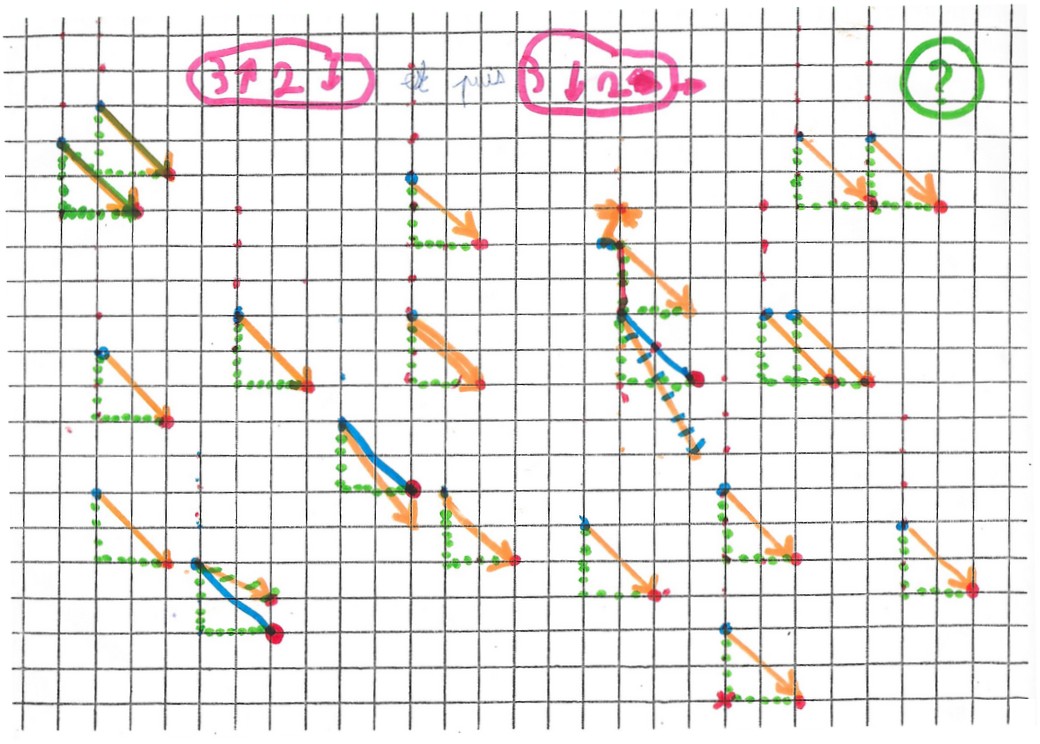
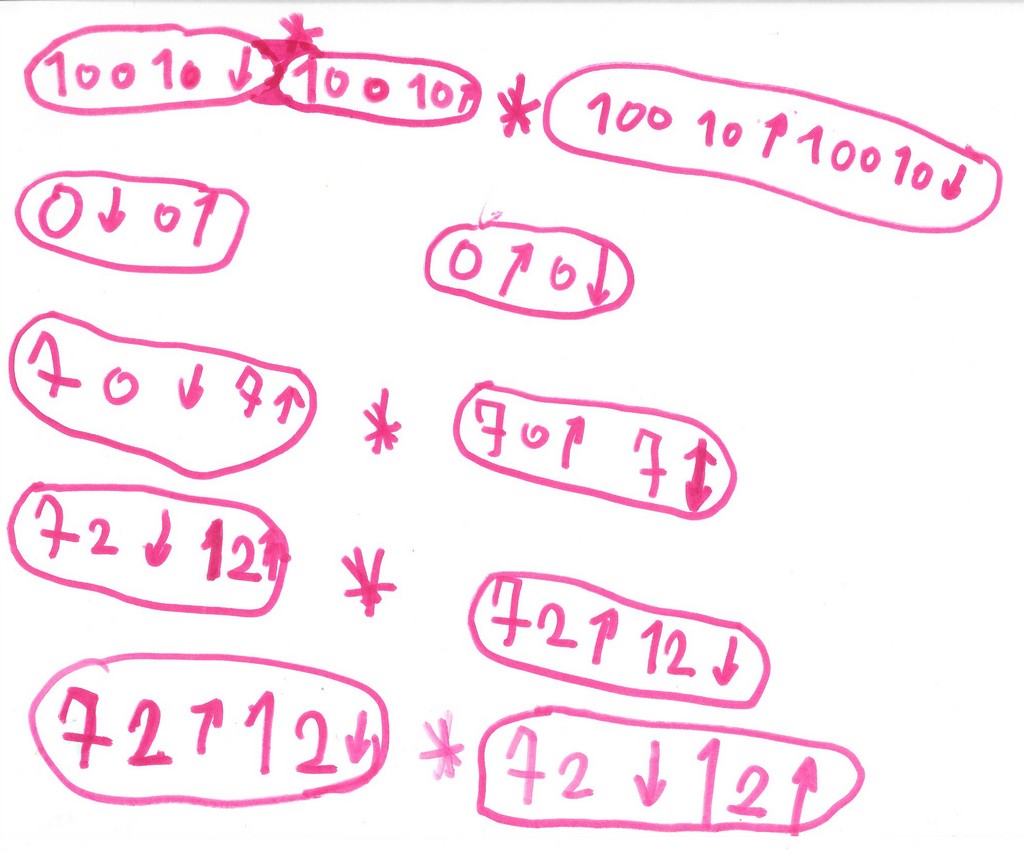
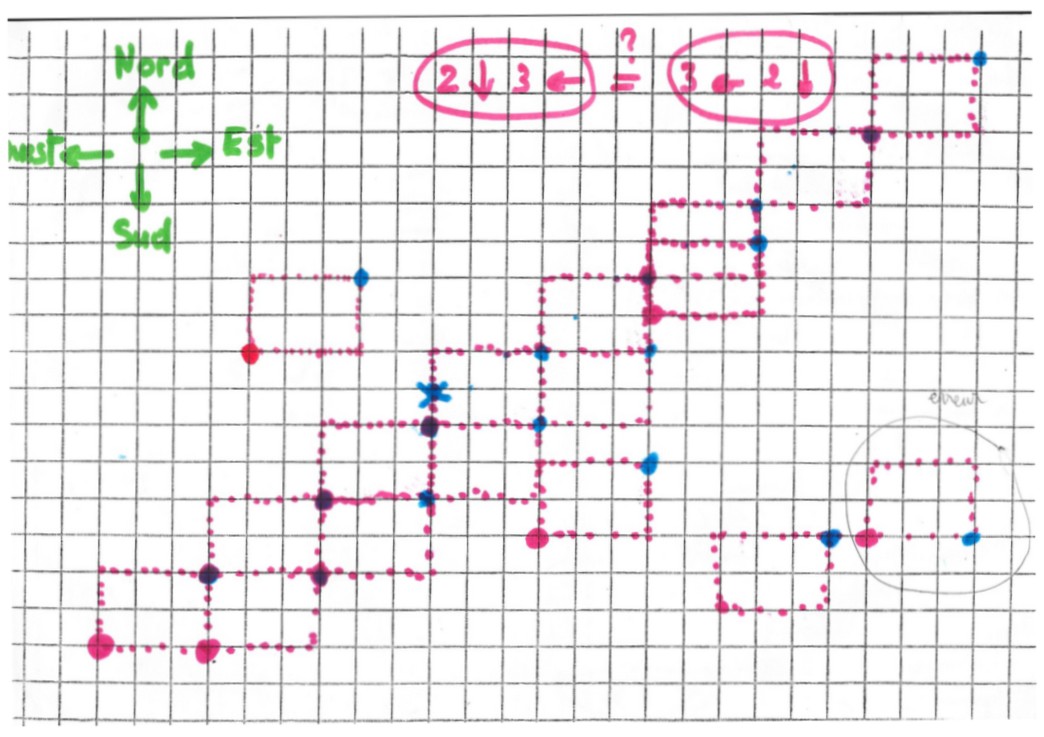
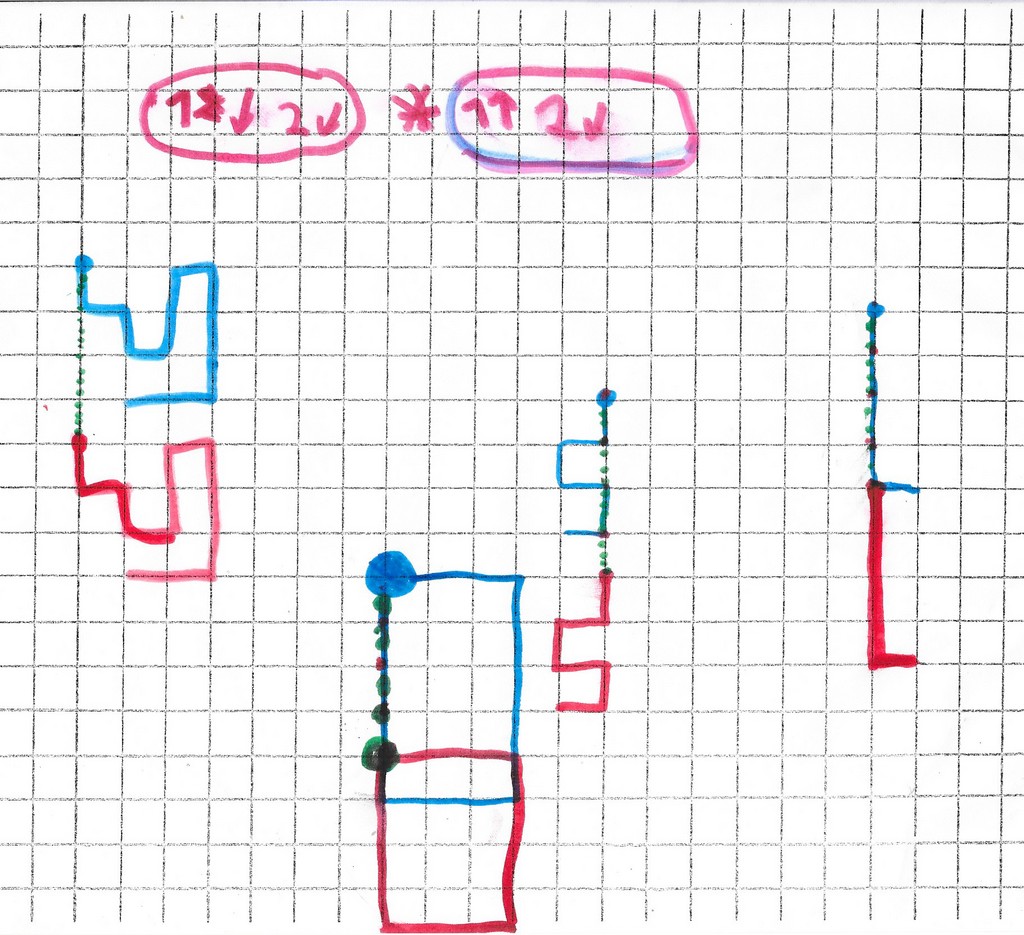
Apparition de la transformation composée
c’est pareil que
Il semble que contrairement à la symétrie (la composée d’une symétrie avec une symétrie n’est pas une symétrie), la composée d’une translation avec une translation est encore une translation.
Est-ce vrai tout le temps ?
Il est important de se poser cette question à chaque fois que nécessaire. Très vite on se sensibilise au problème de la vérité en mathématique, au fait que pour prouver que ce que l’on dit est vrai, il faut que ce soit vrai pour tous les éléments concernés. Mais que pour prouver que quelque choses est faux, il suffit d’un exemple : c’est le problème des quantificateurs ∀ et ∃ (quel que soit et il existe)
Une curiosité ?
Apparition fortuite de la translation identique (futur élément neutre 
) : objet et image sont confondus.
| on peut l’appeler |  |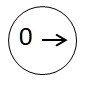
 |
 |
 |
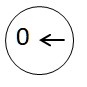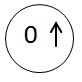| Il décide de l’appeler |  |
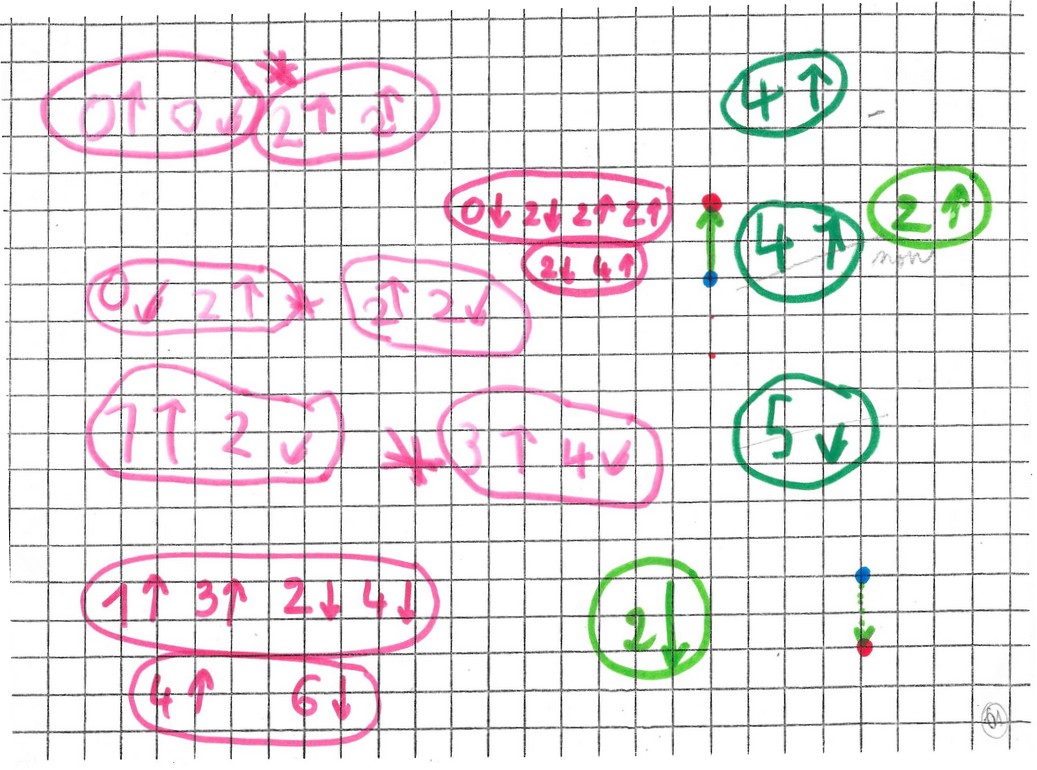
loi de composition et calculs
c’est 
Début d’intuition d’un calcul possible, ce qui laisse entrevoir la possibilité de trouver rapidement la composée.
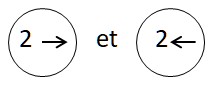s’annulent
Il reste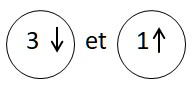 
c’est à dire
Bien sûr, Mickaël prend pas mal de liberté avec la loi d’association *. L’ordre d’effectuation a-t-il de l’importance pour cette loi ? (nécessité d’étudier l’associativité et la commutativité de la loi). Il faudrait aussi voir de plus près les symétriques ainsi que l’élément neutre, c’est à dire étudier les propriétés de (T, *) qui sera le groupe des translations…
à voir dans domaines math/structures
Il s’intéresse à la transformation inverse, celle qui annule.
Premier essai
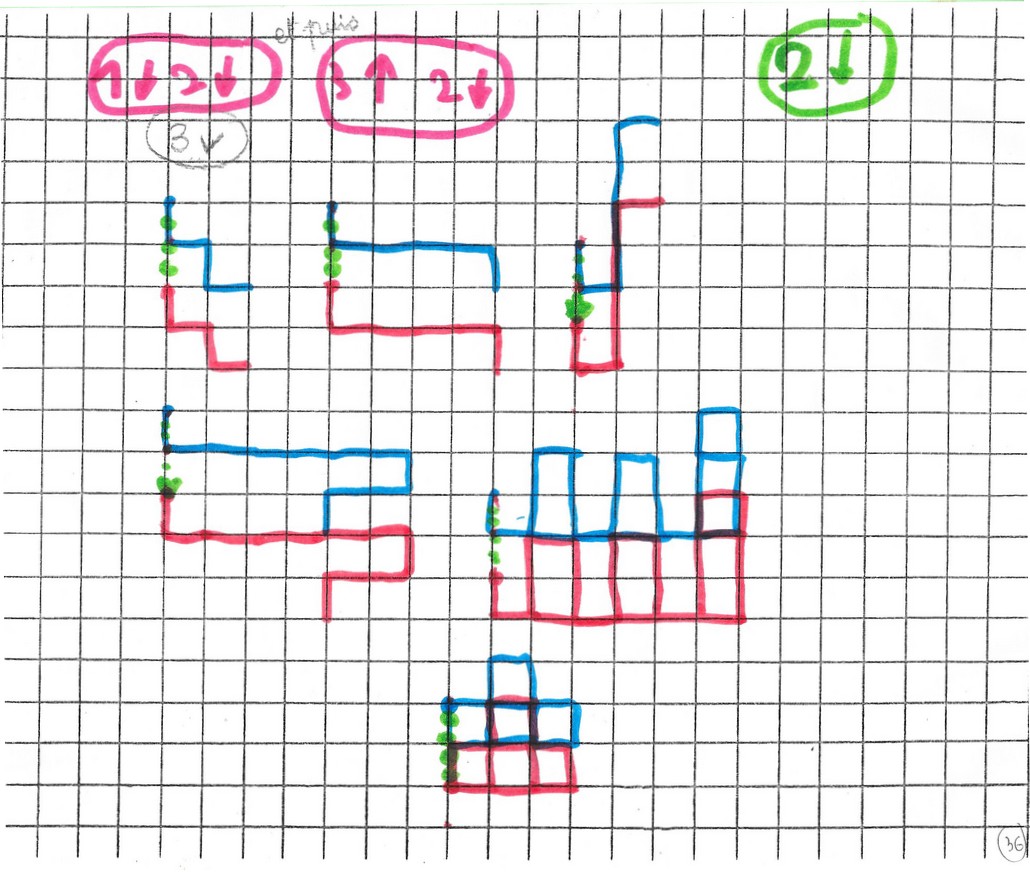
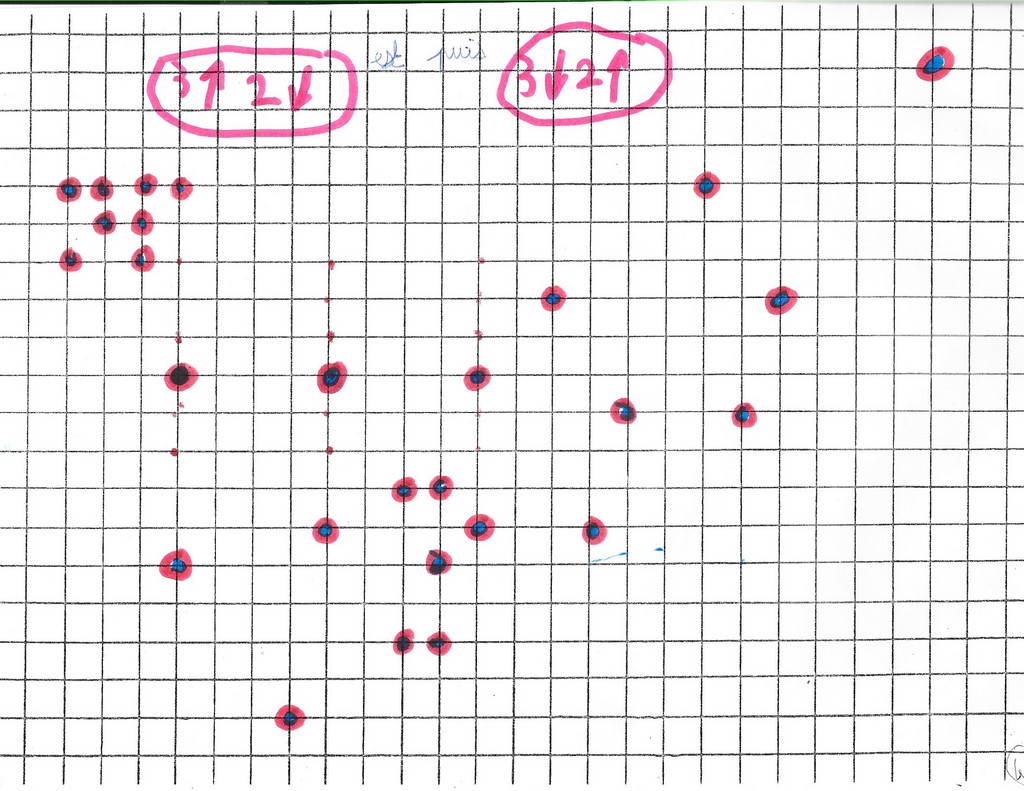
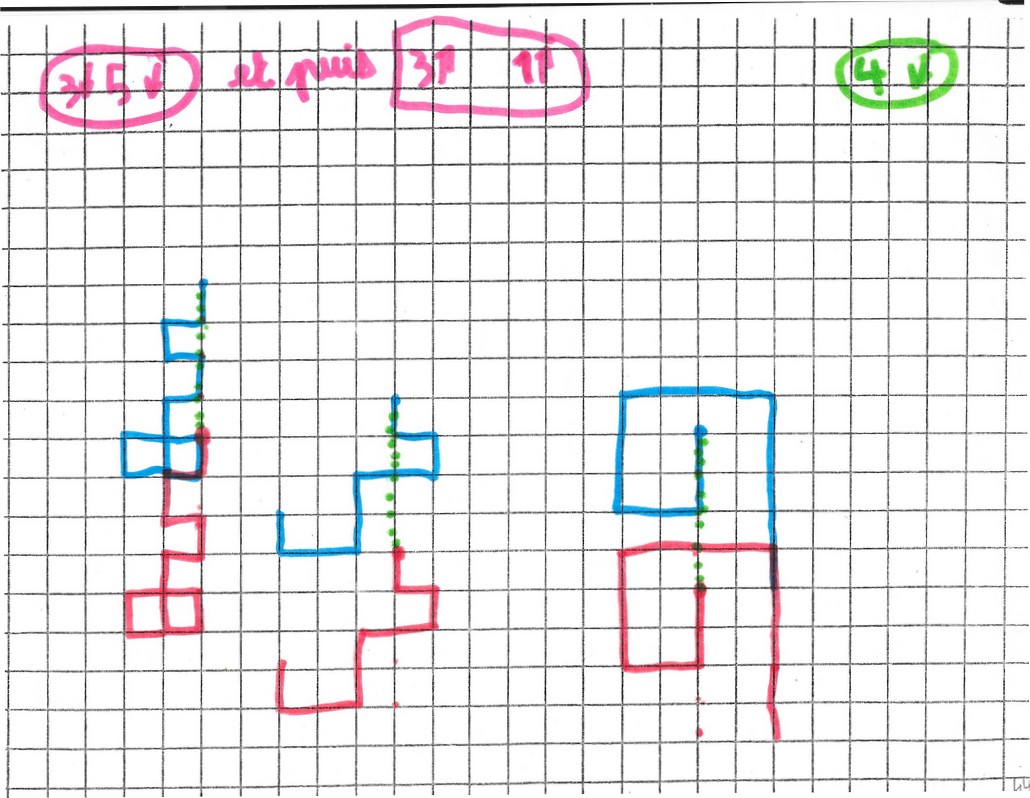
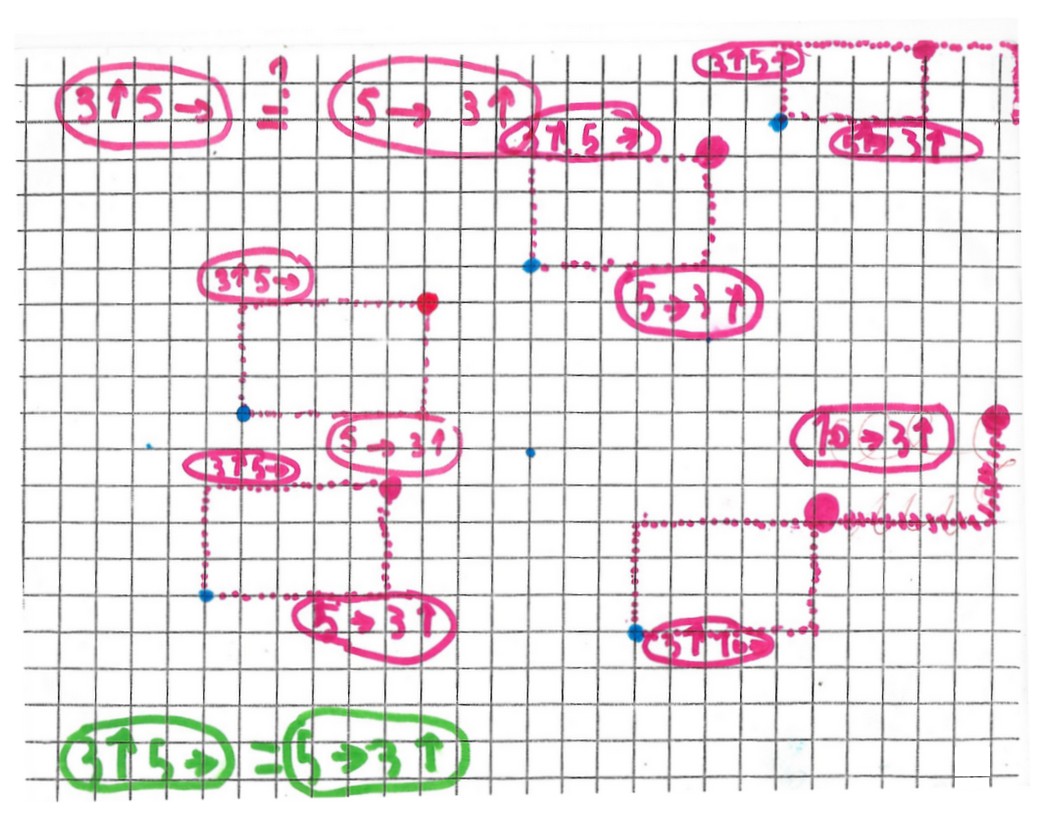
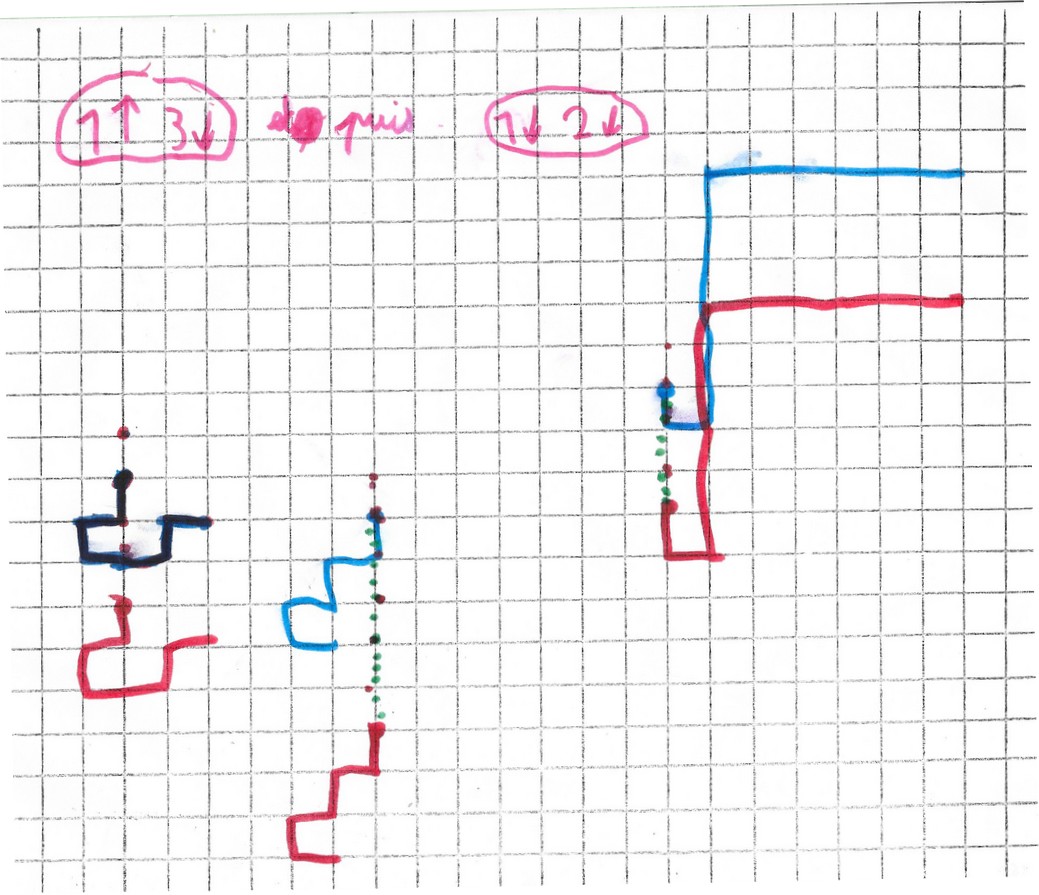
Deuxième essai.
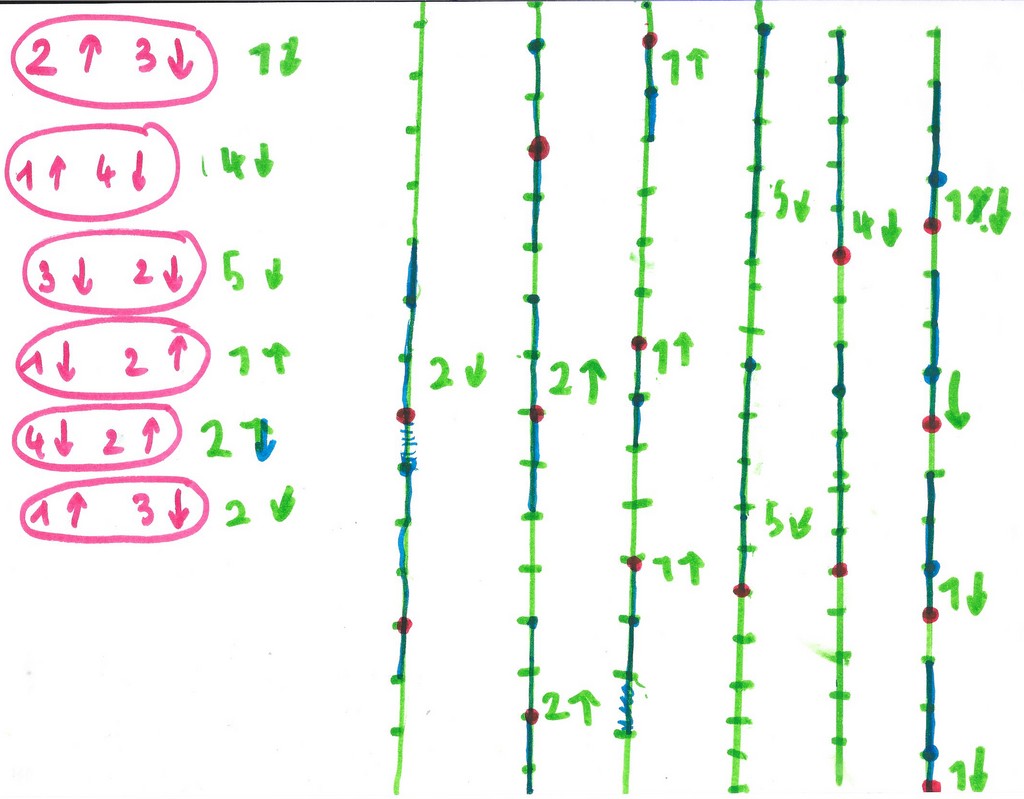
Pour les trois points du centre, il a marqué avec son feutre les cheminements. Pour les autres points, pas de traces. Donc, ou il a fait les chemins mentalement, ou alors, persuadé que ça marche à tous les coups, il a marqué les points images sur les points objets directement.
Là encore, une discussion sur la vérité en mathématique (prouver pour tous les cas) aurait pu avoir lieu.
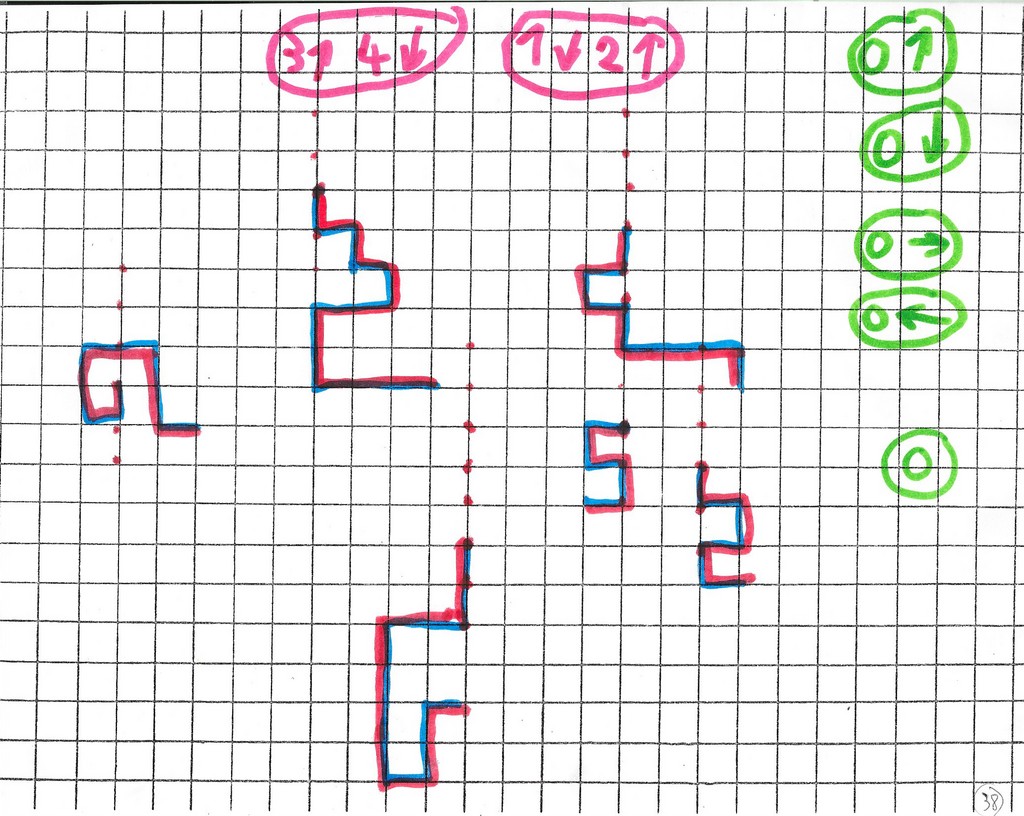
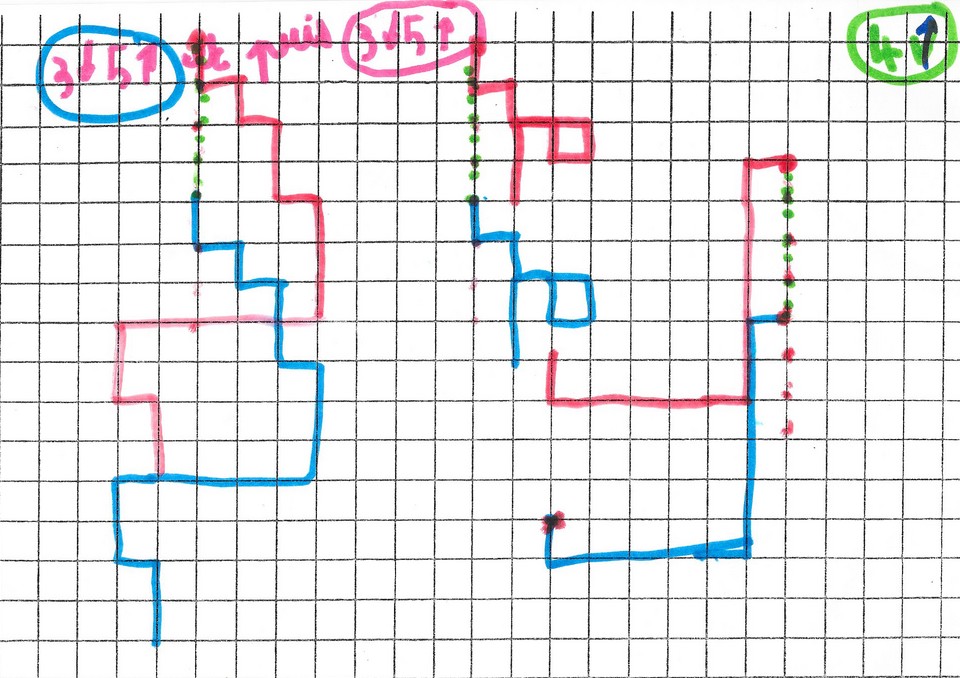
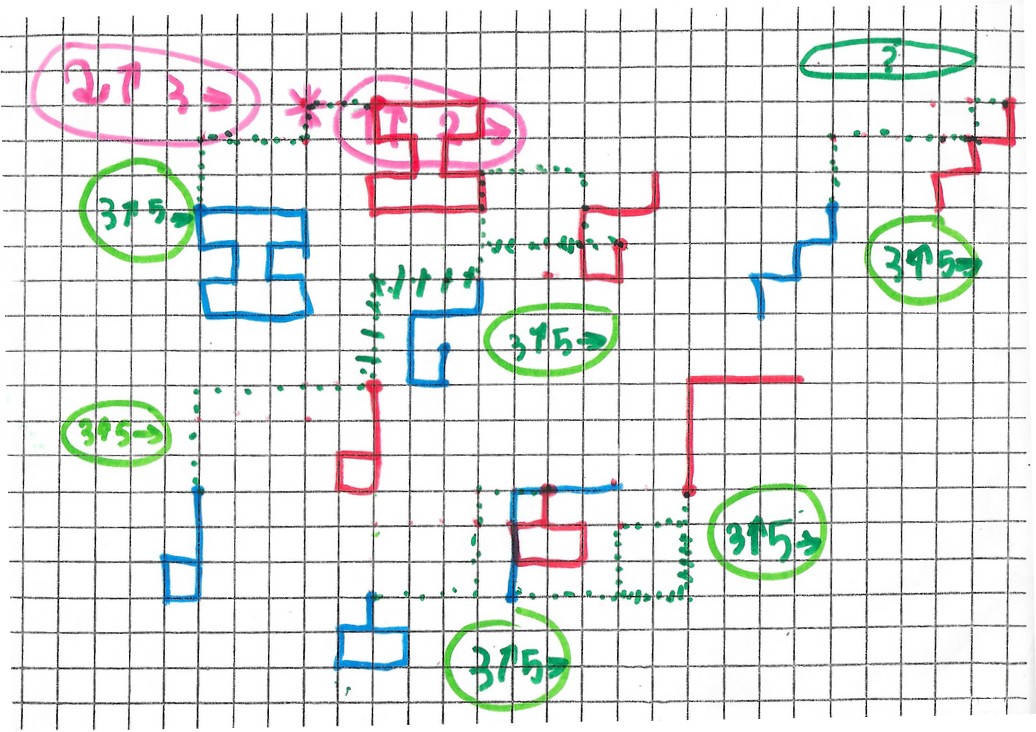
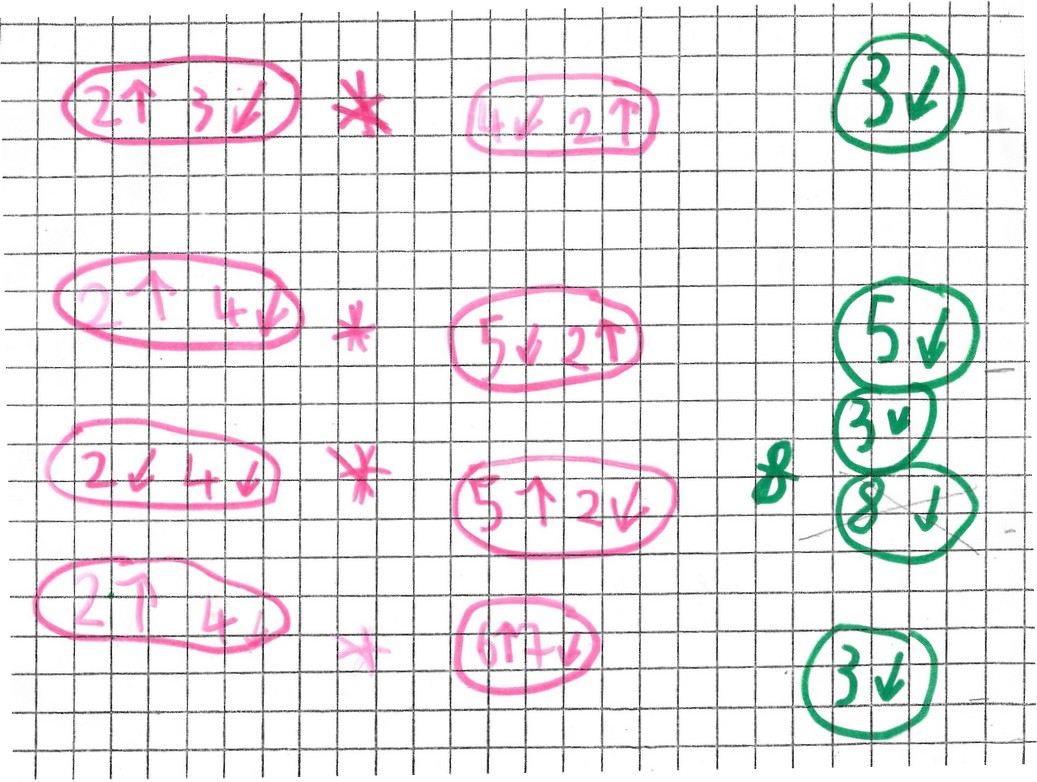
Puis Mickaël se lance dans une tentative de réponse rapide pour la composée :
il essaie d’abord de calculer puis il vérifie par le dessin.
Des erreurs …
| c’est |  |
… mais aussi quelques réussites.
Devant la difficulté, il revient sur un terrain plus connu …
… tout en se donnant prudemment quelques frissons.
L’expression « et puis » est symbolisée par *, loi de composition.
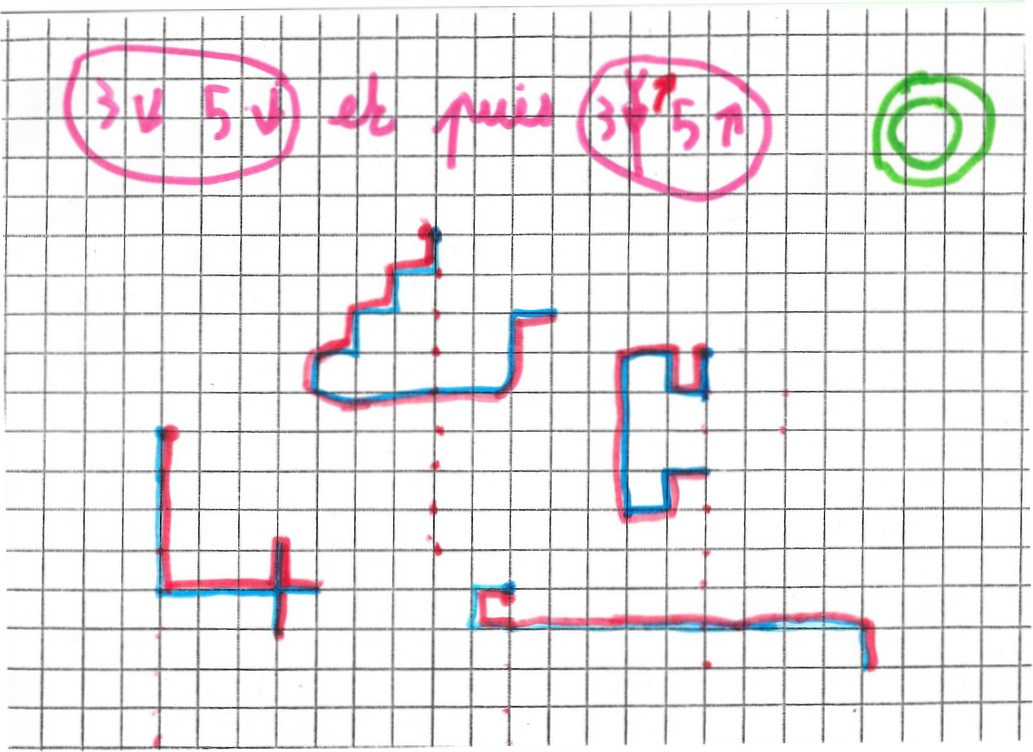
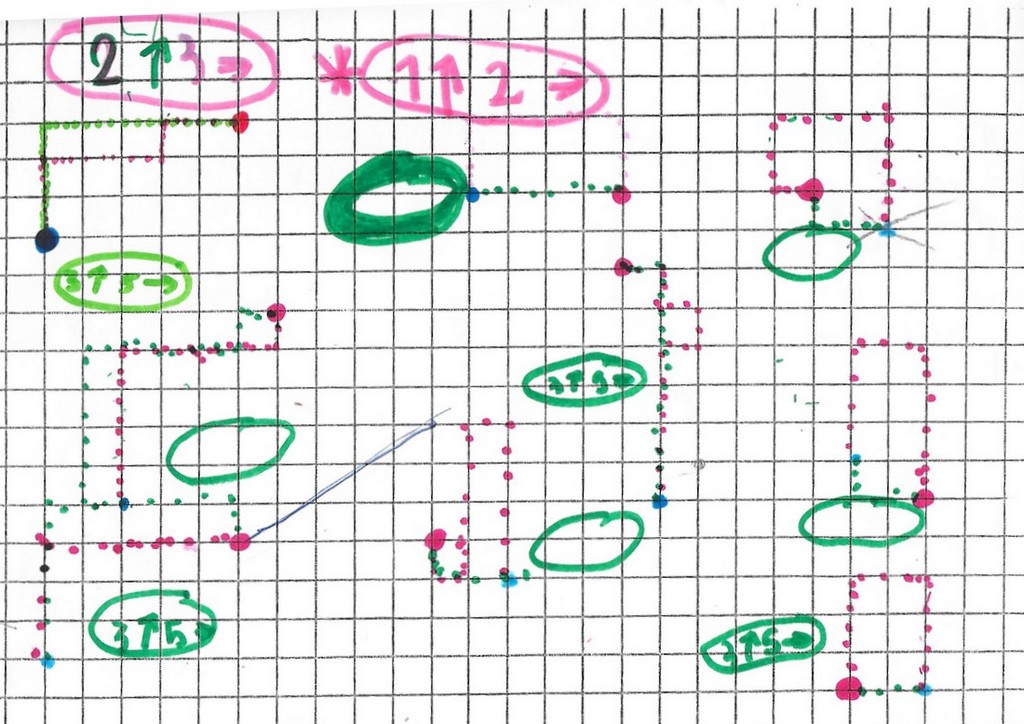
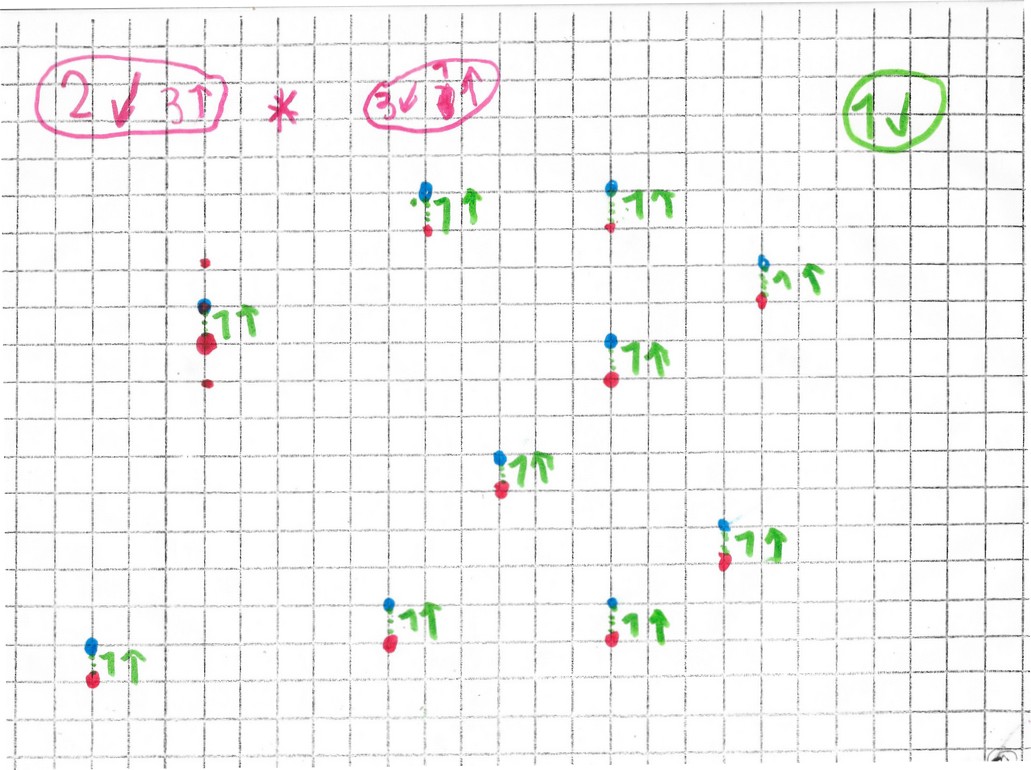
Après plusieurs exemples, Mickaël remarque que « ça ressemble à la symétrie » :
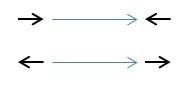
mais aussi en plus
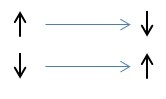
Et on conserve le nombres de pas.
J’interviens :
| On dit que la flèche |  |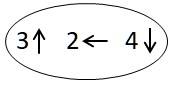
est la symétrique de |  |
parce que la composée, c’est | |
Autre question sur l’ordre qui le turlupine :
Michaël reprend un problème laissé de côté (?) : le calcul de la composée : T * T’ = ?
Je lui conseille de n’utiliser pour l’instant que → et ↑ .
Prudent, il passe d’abord par le dessin pour donner la réponse.
Puis il constate que finalement, en n’utilisant que les directions ↓ et ↑, il peut toujours calculer la transformation composée.
Pour aller plus vite, il ne s’intéresse qu’aux points de départ, sachant qu’il n’y aura pas de problèmes sur le chemin lui-même.
Nouveaux essais sans dessin
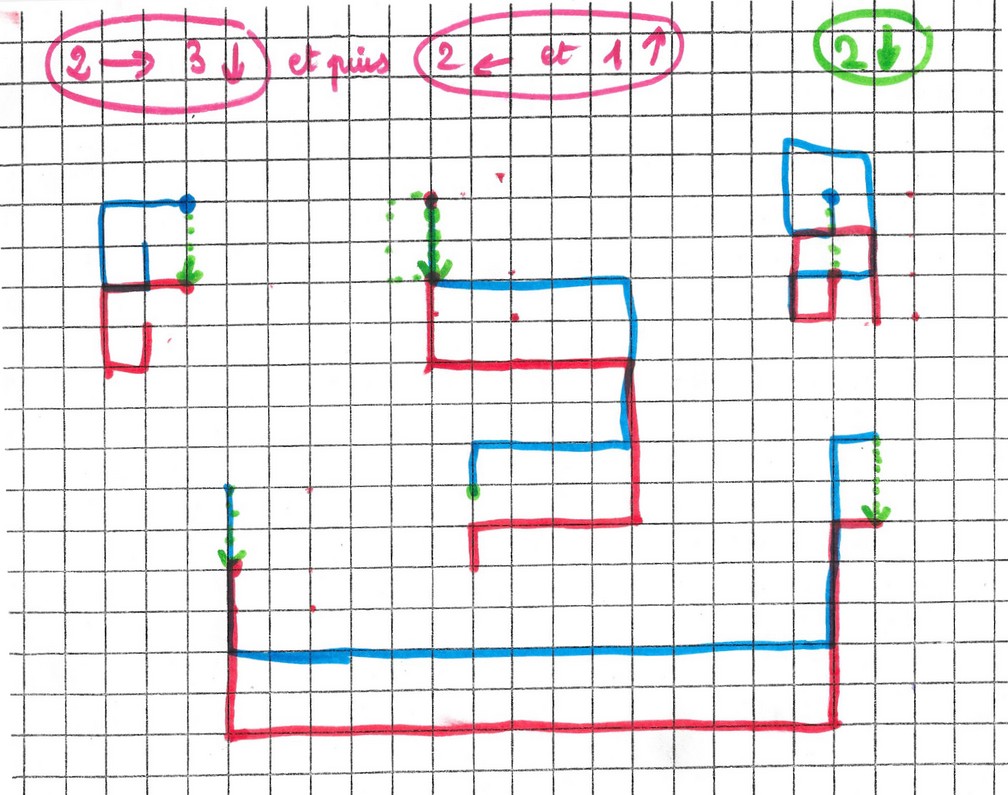
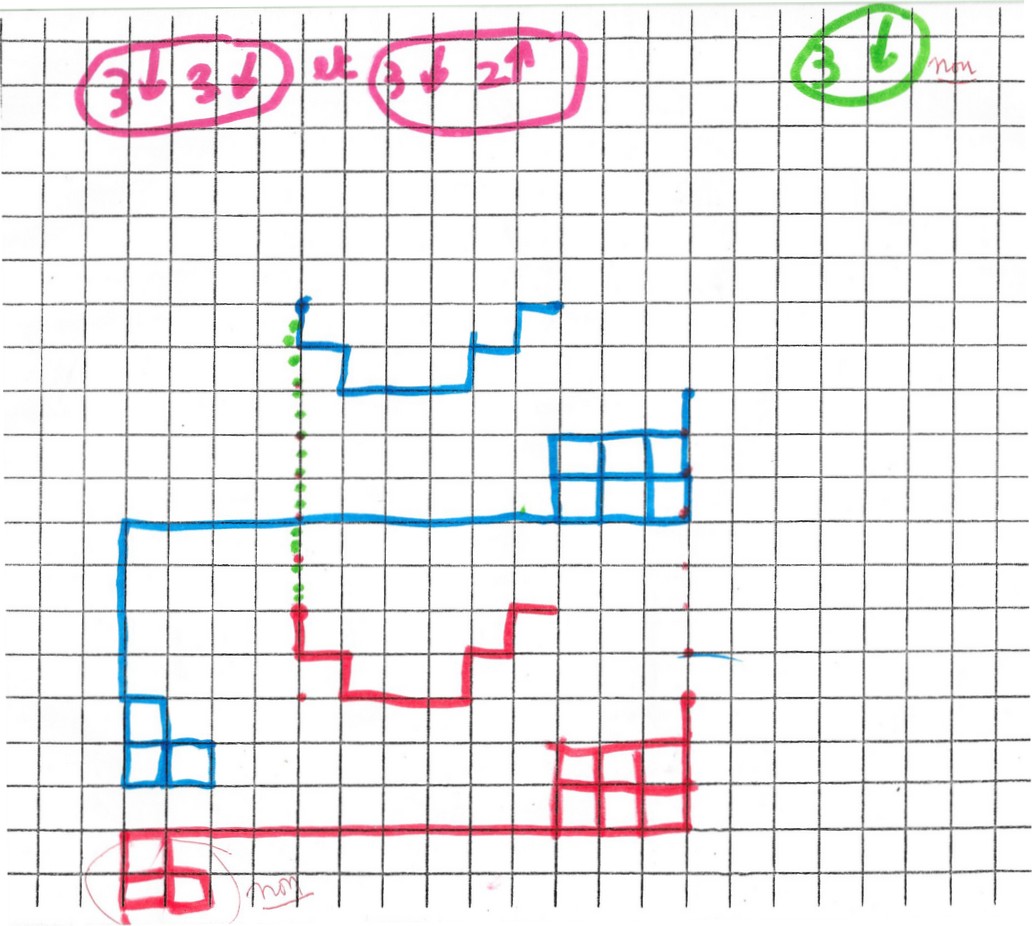
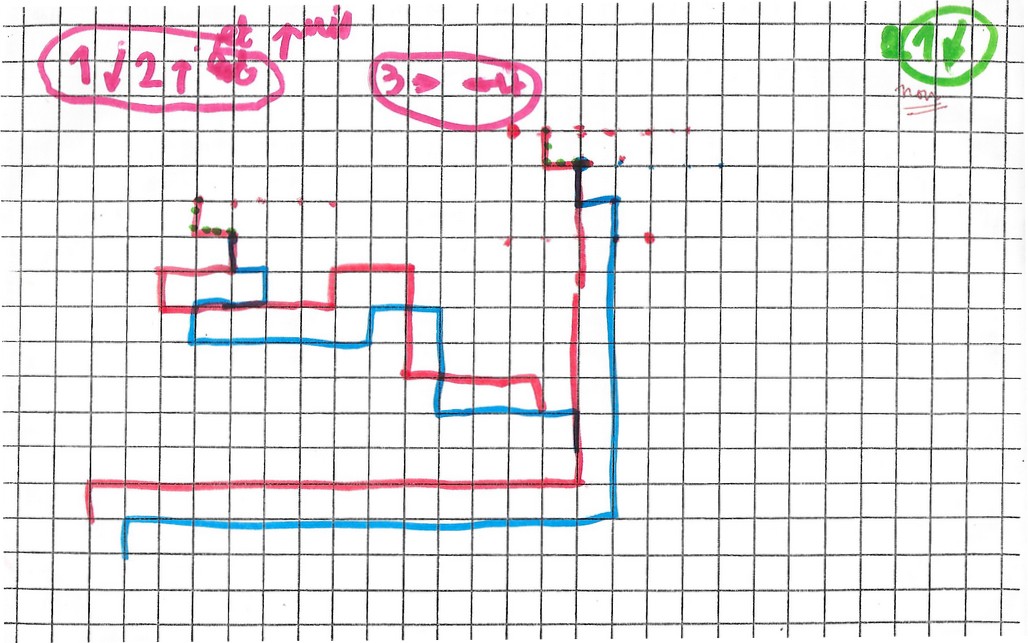
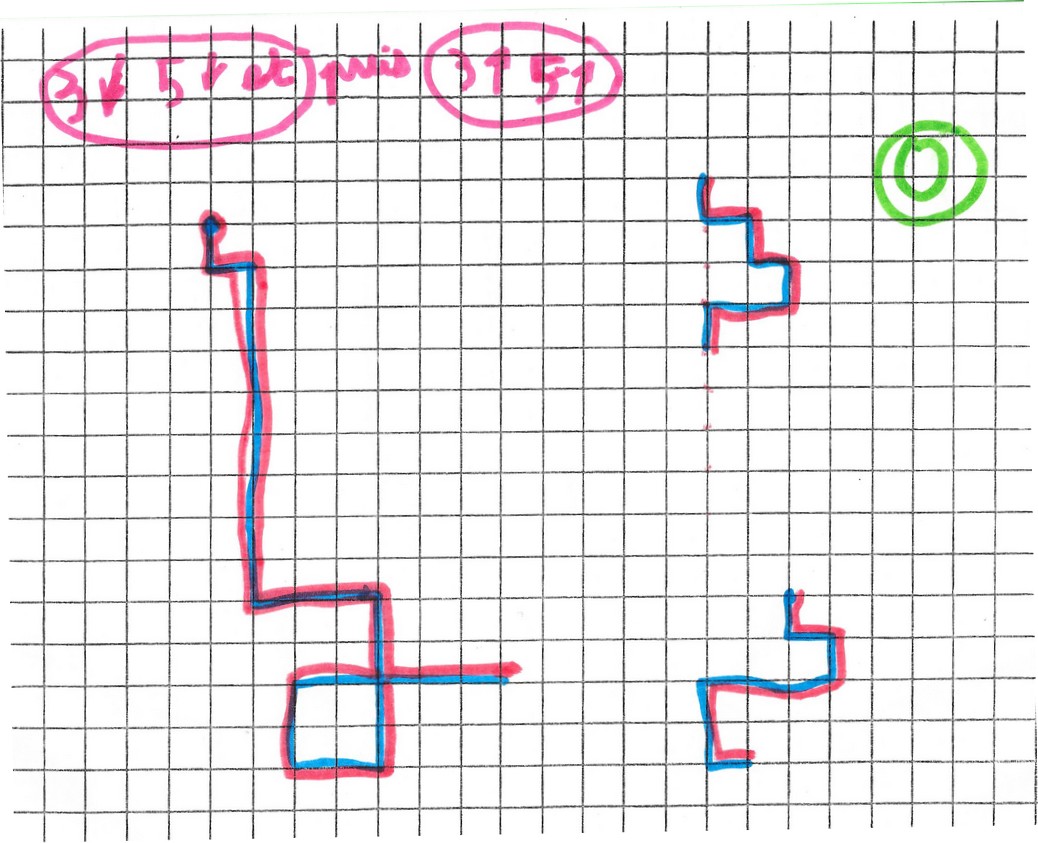
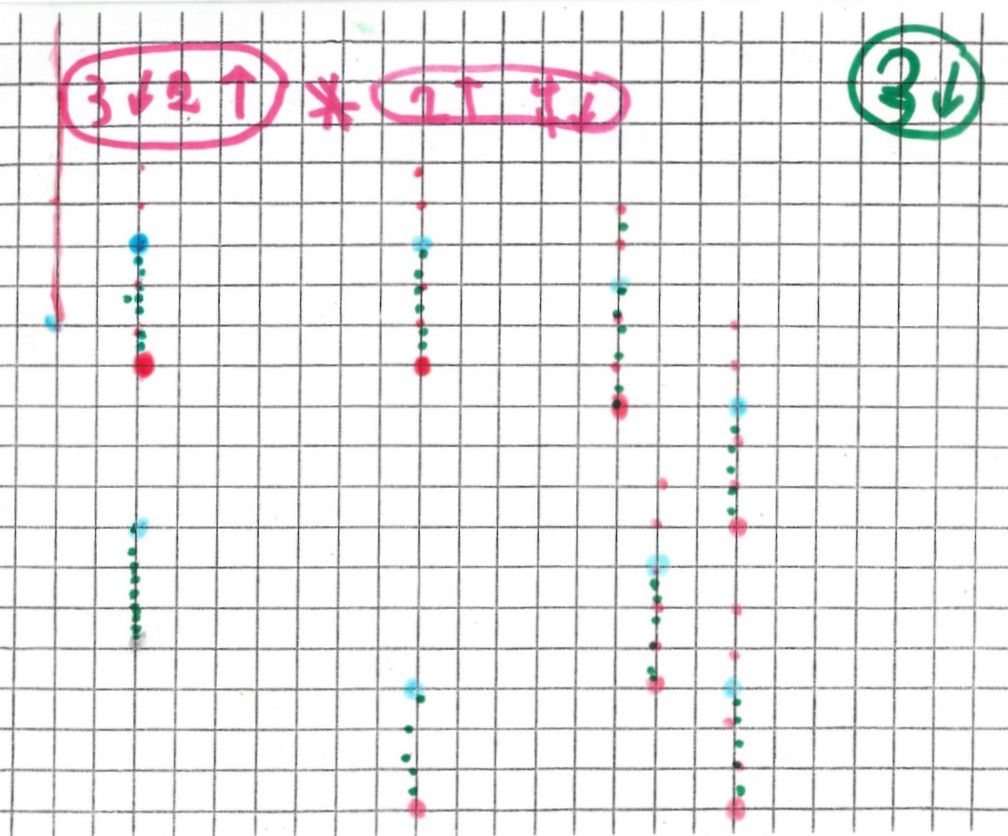
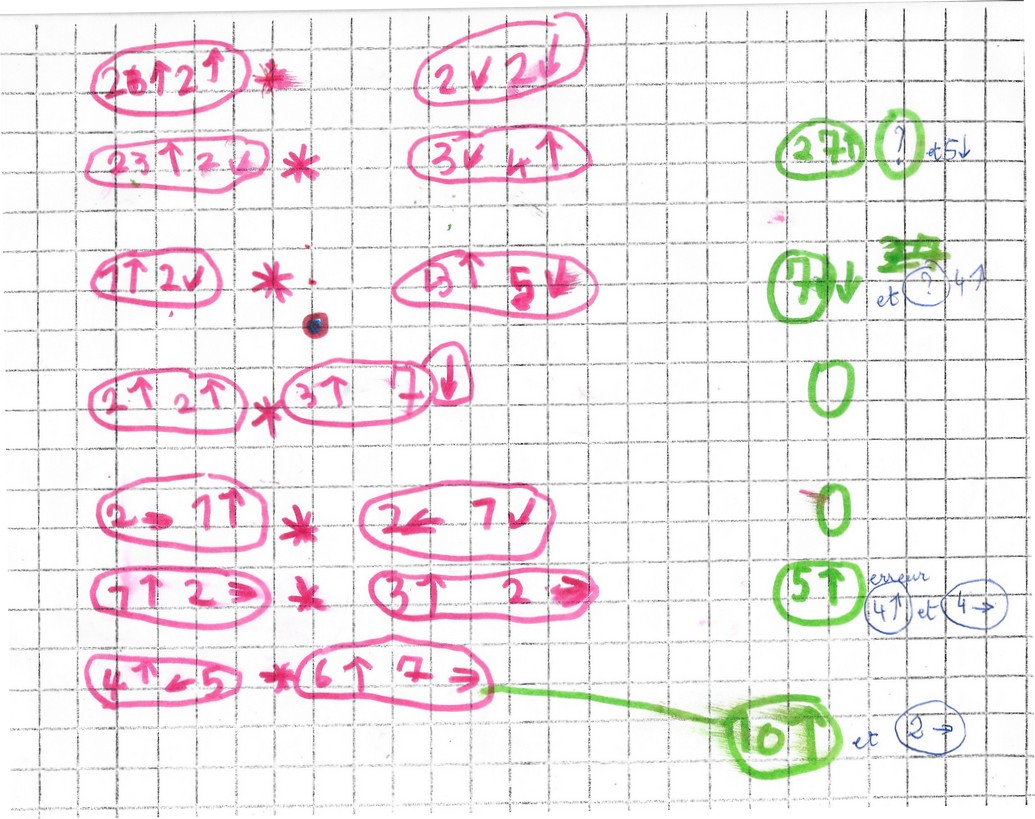
Tentatives plus compliquées mais difficultés…
Michaël a du mal à gérer toutes les directions à la fois. Il vaut mieux simplifier pour l’instant et n’utiliser que les directions horizontales et verticales ensemble.
Je lui propose une technique : le calcul par flèche, dans le sens de la lecture, que l’on fait ensemble :
On simplifie donc les translations.
Mickaël utilise la ligne graduée pour s’aider.
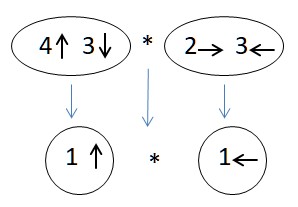
Et là, un autre travail peut commencer. Bien sûr, le travail sur la translation n’est pas terminé. Mickaël ne sait pas encore faire de translations sans machine. Mais dans ce domaine, d’autres enfants de la classe travailleront certainement le sujet, ou peut-être qu’il reviendra sur le sujet à partir d’autres situations différentes. Et il est probable que lors de leurs présentations, Michaël sera très attentif et intègrera peut-être l’expérience des autres sans forcément en avoir fait les tâtonnements. Il sera perméable à leurs connaissances. Il sera disponible.
C’est cette disponibilité qui permet de bénéficier du patrimoine culturel de la classe, mais aussi de la classe des correspondants.
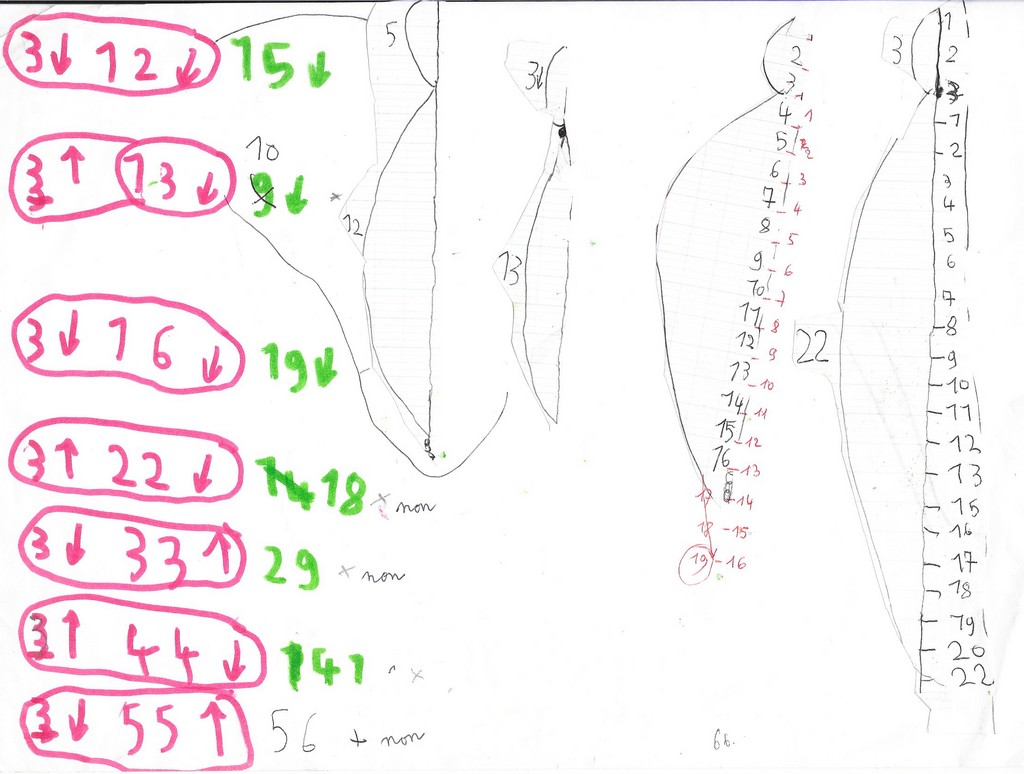
De nouvelles difficultés, mais aussi de nouvelles découvertes vont se présenter :
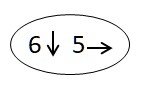
La présence des numéros perturbe la vision pour faire 3→ et 16 →
La position s’appelle 16 si on part de 0. Il est nécessaire ici de changer de point de départ.
Le nouveau point de départ est 3 :
0 ————————-> 3
1 ————————-> 4
etc..
16 ———————–> ?
On s’oriente vers la fonction 3 de plus. On retrouvera la même structure que pour la translation :
– changement de point de départ
– les actions sont conservées entre le monde de départ (objet) et le monde d’arrivée (image) *
* voir étude des fonctions numériques additives dans domaines maths / maths numériques / fonctions numériques