L’hypothèse d’Arthur
classes de cycle II et III : CP- CE1-CE2 | 6/9 ans | école 3 classes + 2 maternelles
recherche collective et individuelle
connexions : fonctions numériques, fonctions multiplicatives
Le contenu de la page
- les moitiés
- exploration verticale, loi de décomposition
- paquets et moitiés
Les moitiés
Connaître les moitiés des petits nombres, à 7/8 ans, certains maîtrisent. (3 c’est la moitié de 6 parce que 3+3=6). Mais dès que les nombres augmentent, la difficulté surgit.
Pour vérifier l’hypothèse d’Arthur, on a besoin de beaucoup de nombres et de leur moitié. La construction d’une technique opératoire efficace et sûre pour trouver la moitié de n’importe quel nombre naturel n’est pas encore à notre portée.
Une première technique
L’ idée est de chercher des résultats en tâtonnant à partir de résultats connus : moitié de 26 ?
Je sais que la moitié de 20, c’est 10 ; 10+10=20.
Donc la moitié de 26, c’est un peu plus grand que 10.
11+11=22 ; 12+12=24 ; 13+13=26 !
13 est la moitié de 26.
Certains s’essaient à cette technique qui va poser assez rapidement de nouveaux soucis.
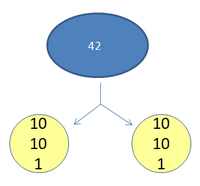
Les représentations évoluent avec la montée en abstraction : du dessin fidèle des éléments (6 ans) à l’utilisation des nombres, la technique opératoire se construit, s’affine progressivement avec pour moteurs le besoin de fiabilité, d’économie et de rapidité.
voir les fonctions dans domaines math
Exploration verticale, loi de décomposition
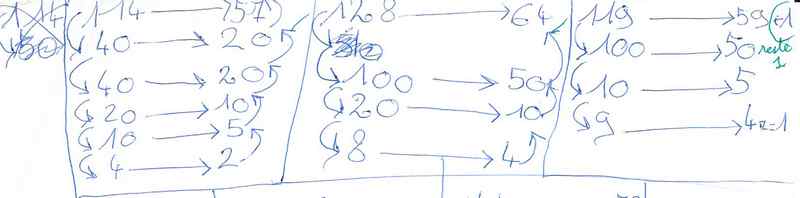
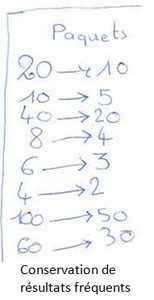
Les premiers essais de vérification d’Arthur :
il emploie la méthode du calcul des paquets de 2. (perles –> paquets de 2 perles) en utilisant la décomposition du nombre choisi : 114, c’est 40+40+20+10+4. Il admet implicitement aussi qu’à la situation 40+40 dans le monde des perles correspond une autre situation similaire : 20+20 dans le monde des paquets : l’addition se conserve.
Il utilise une « exploration verticale ». (voir domaines math/généralités)
Par souci de rapidité, il conserve et utilise certains résultats découverts (20,10, 100,..). Cette liste sera extrêmement importante pour la suite.
Il lui suffit ensuite de vérifier manuellement ou avec la calculette si nécessaire :
64+64=128
Un peu plus délicat pour les nombres impairs :
57+57 = 114 ; (59+59)+1 = 119
Paquets et moitiés
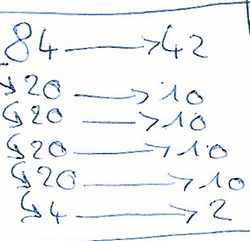
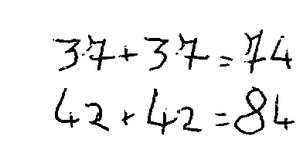
Après de nombreuses vérifications par addition, le nombre de paquets et la moitié, c’est toujours le même nombre.
