Le contenu de la page
4. la recherche : deuxième défi
5. un prolongement

Deuxième défi
Le premier album pour les corres explique chaque attraction de la ducasse.
Voici les feuilles pour le tiercé à lapins :
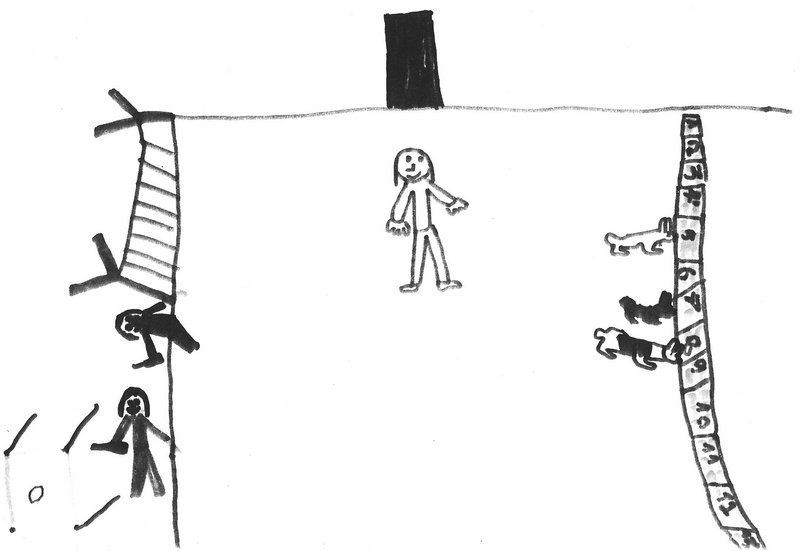
Le moteur de la correspondance scolaire détermine la suite de la recherche. Après s’être intéressé aux enfants, on se focalise cette fois sur les attractions.

Il faut aussi envoyer un album aux correspondants pour rassembler tous les résultats en les regroupant sur une feuille par attraction. On se partage le travail et chacun se choisit une attraction. Voici les deux feuilles pour le petit manège :


Voici les feuilles pour la marchande de bonbons :

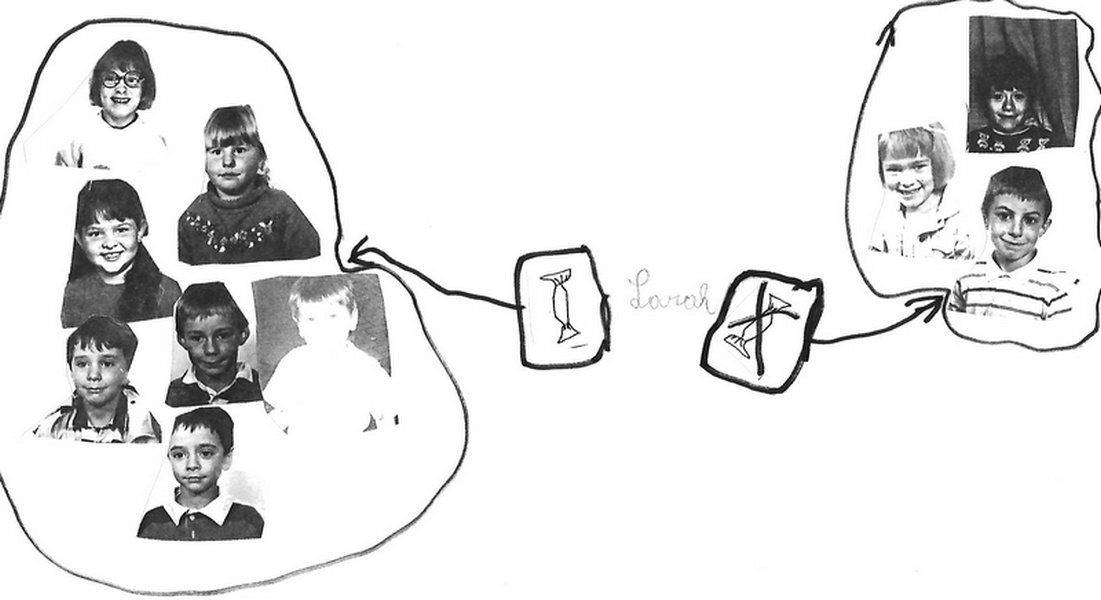
Les essais aboutissent à la découverte de deux représentations :
– le diagramme de Venn-Euler
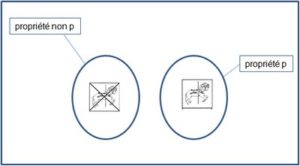
p : « est allé au petit manège »
– et une autre représentation, les couples enfant-propriété, qui préfigure la naissance du diagramme sagittal qui sera découvert peu après, selon le principe d’économie :
On n’utilise plus qu’une seule fois les deux logos p et non p, et une flèche indique la relation. La flèche, elle aussi, a une histoire. Cet outil a été construit à l’occasion d’une recherche sur le problème de la représentation dans une situation, de ce qui est premier et de ce qui est deuxième, de l’avant et de l’après …
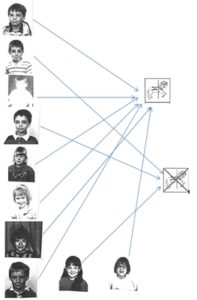
Maintenant, l’idée est d’avoir toutes les feuilles d’attraction en même temps. Il faut simplifier pour tout avoir sur la même feuille.
Pour aller plus vite :
– chaque enfant est représenté par la première lettre de son prénom (il faut régler deux soucis : Sarah et Stéphanie, et Matthieu et Marie).

– et ne représenter les attractions qu’une fois.
On prend la bande de ducasse :
![]()
Et chacun inscrit son initiale en-dessous de chaque attraction faite :
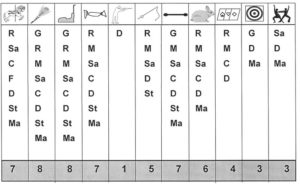
Il faut représenter la fréquentation de toutes les attractions
On s’aperçoit encore une fois que l’idée d’utiliser une bande de ducasse ordonnée est bonne. Elle permet d’observer des choses.
Avec l’utilisation de la deuxième lettre du prénom (Sa, St, Ma) s’ouvrent de nouvelles perspectives de réflexion et de recherches :
– comment différencier deux éléments distincts qui portent la même dénomination ?
Dans les familles, tout le monde porte le même nom, et on différencie les individus par un deuxième mot : le prénom.
Dans la classe, quand deux enfants portent le même prénom, il faut ajouter un renseignement pour pouvoir les différencier.
– quelquefois, un élément porte plusieurs noms différents : Guillaume, c’est le fils de …, c’est le frère de …, le copain de …, le voisin de … Comment fait-on pour savoir qu’on parle de la même personne ? (utilisation du concept d’égalité)
– pour les jours, il faut écrire le nom, son numéro, le mois et des fois l’année.
– les nombres ont eux aussi plusieurs noms différents, suivant la situation : 6, 4+2, 7-1, etc.
L’impression que beaucoup d’enfants sont allés aux autos tamponnantes se confirme. Mais avec le comptage, on en est sûr. On a cherché toutes les informations sur tous les enfants et toutes les attractions. On n’a rien oublié.
Et maintenant, on peut dire avec certitude des choses qui sont vraies.
Les nombres sont bien utiles : on est sûr dire de ne pas dire de choses fausses. On sait quelle attraction a eu le plus de succès, ou le moins.
Autre représentation :
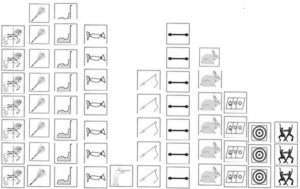
Les attractions rangées par ordre de préférence :
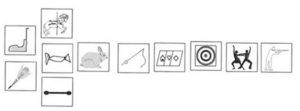
Peu à peu une prise de conscience émerge : une démarche rigoureuse de recueil de données, de leur conservation et de leur organisation permet de décider avec certitude si telle affirmation est vraie ou telle autre fausse.
Retour au tableau des bandes de ducasse
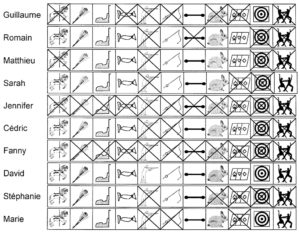
Vers la découverte du tableau cartésien, un outil très utilisé en école maternelle et qui cache bien des implicites…
La découverte active de ce tableau à double entrée fait apparaître clairement son utilité en tant qu’outil de résolution de certains problèmes et facile son réinvestissement dans de futures situations à traiter.
Chaque bande de ducasse donne tous les renseignements concernant les attractions faites par chaque enfant. Il suffit de lire le prénom de l’enfant et sa ligne. De près, ça va ; on peut suivre la ligne avec le doigt. Mais de plus loin, on s’y perd un peu… Les logos et les lignes se mélangent un peu. Il faut trouver plus simple.
Une remarque :
Si on lit en descendant, la première colonne ne parle que du petit manège, la deuxième que des fléchettes, … et on n’a que deux possibilités à chaque fois : l’enfant a fait ou pas l’activité. C’est oui ou non. Si oui ou non remplacent les logos, peut-être que ce sera plus clair. Mais il faut laisser en haut de chaque colonne le picto une fois pour savoir de quelle attraction on parle.

Le tableau avec tous les oui et les non, ce n’est pas mieux !
On peut enlever tous les oui et ne garder que les non ; ça ira quand même : quand c’est écrit non, c’est qu’on n’a pas fait l’attraction. Et quand ce n’est rien écrit, c’est que c’est oui.

On arrive mieux à lire, mais tous les non, c’est long à écrire ! On peut les remplacer par des croix qui veulent dire non comme sur le logo barré.

Quelqu’un a dit : « Oui mais quand on doit remplir un questionnaire, il faut cocher les cases, ça veut dire faire une croix, pour dire que c’est vrai. Donc la croix, elle veut dire oui.
Changement de tableau donc :

Ce tableau donne tous les renseignements :
– si on lit en descendant (en colonne : on dit verticalement), on sait tout sur les attractions ;
– Et si on lit en ligne (horizontalement), on sait tout sur les enfants.
Un prolongement
On a remarqué certaines choses :
La ligne de David est remplie de croix : il a tout fait ! ça se voit sur sa bande de ducasse :

La ligne de Jennifer, c’est tout le contraire de David.

On a fait des bandes contraires, des lignes contraires, des colonnes contraires.. et plein d’autres choses contraires :
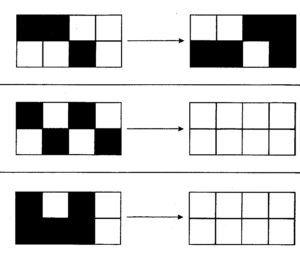
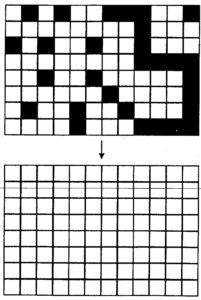
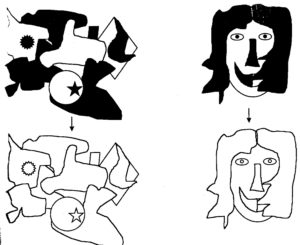
Rappel :
Ceci est le témoignage d’un déroulement de recherche mathématique avec cet événement au départ : la ducasse et une problématisation de la situation corrélée aux besoins, aux interrogations du moment. De nombreux autres scénarios auraient pu se dérouler avec des défis initiaux différents, d’autres élèves, à un autre moment, etc.
La recherche s’est faite en groupe parce que tout le monde était concerné.
C’est une recherche collective, qui en réalité, est un ensemble de recherches individuelles (chacun cherche de son côté puis partage ses résultats lors de moments fréquents de présentation au groupe).
C’est une recherche avec un sujet unique et des objectifs de recherche communs.
De nouvelles pistes se sont ouvertes :
Existe-t-il d’autres couples de bandes de ducasse contraires ? (pas traité)
Les contraires (blanc, noir) et l’idée sous-jacente de condition, de déterminisme : si c’est blanc, alors ce sera noir ; si c’est noir, alors ce sera blanc. De nombreuses variations de critères à deux valeurs sont possibles : changer avec deux autres couleurs, deux autres formes, mais aussi trois autres couleurs, transformations de formes… C’est le domaine du changement déterminé, le très vaste domaine mathématique des fonctions.
tissu « pied de poule » :

MC Escher : « jour et nuit »

